Как определяется погрешность измерений цифрового прибора

Максимальная абсолютная погрешность

Процесс зфавновсшивагия в цифровых приборах развертывающего уравновеши.

В цифровых циклических приборах выходной код N приближается к искомому отсчету Nх с одной стороны, сверху или снизу, поэтому при АХп ч 0 максимальная абсолютная погрешность от квантования равна ступени & хк.
 

Здесь: Арн — максимальная абсолютная погрешность величины рн, равная половине единицы разряда последней значащей цифры в табличном значении рн; Ар и АГ — максимальные абсолютные погрешности измерения р и Т соответственно.
 

Абсолютная погрешность температурного предела смеси при использовании в расчете надежных экспериментальных данных по давлению пара чистых компонентов, растворимости и коэффициентам активности, как правило, не превышает максимальной абсолютной погрешности температурного предела компонентов смеси.
 

Абсолютная погрешность при изображении в ячейке чисел с запятой, фиксированной после определенного разряда, не превосходит по величине единицы младшего разряда, то есть, как говорят, максимальная абсолютная погрешность при этом постоянна.
 

Для учета в модели однократной экстракции NRTL влияния воды, были дополнительно подобраны эмпирические коэффициенты бинарного взаимодействия воды с компонентами системы, применение которых при численных исследованиях существенно уменьшило погрешности моделирования в области содержания воды в экстрагенте выше 8 % об. По выходу рафината и содержанию в нем аренов максимальные абсолютные погрешности в этой области составляют 0 6 и 0 9 %, соответственно. Погрешности расчета по выходу экстракта и содержания в нем аренов снизились до 0 6 и 1 1 %, что составляет 4 8 и 1 4 % относительной по.
 

Следует отметить, что для измерения среднего фазового сдвига рассмотренным методом характерно уменьшение погрешности дискретности по сравнению с имеющей место при измерении одиночного интервала времени. Хотя максимальная абсолютная погрешность дискретности определения длительности одного интервала АГ составляет ГСЧ, результирующая погрешность за время измерения Ткзм уменьшается, так как результаты измерения всех k интервалов АГ суммируются, а возникновение частотной погрешности дискретности положительного или отрицательного знака равновероятно.
 

Рассмотрим погрешность от квантования. Следовательно, максимальная абсолютная погрешность от квантования будет равна единице.
 

Второй способ сводится к увеличению числа импульсов, заполняющих временные ворота, достигаемому умножением частоты исследуемого сигнала. При этом максимальная абсолютная погрешность меняется ( если неизменна длительность ворот), но уменьшается относительная погрешность. Осуществление данного способа сопряжено с применением дополнительного блока — умножителя частоты, что усложняет и удорожает аппаратуру.
 

Максимальную погрешность Дгд Т0 удобно учитывать через эквивалентное случайное изменение числа счетных импульсов Nx на 1 импульс. При этом максимальная абсолютная погрешность дискретизации может быть определена разностью значений частоты / получаемых по формулам (7.4) или (7.5) при Л 1 и Nx, и равна А.
 

Максимальные абсолютные погрешности показаний манометров Мп и Мв, исправленных на систематические погрешности приборов, принимаются равными 0 2н — 0 5 цены наименьшего деления шкалы, если эта величина не превышает вариации показаний прибора. В противном случае максимальная абсолютная погрешность равна вариации показа ний прибора, которая определяется при тарировании.
 

Максимальные абсолютные погрешности показаний манометров М и Мв, исправленных на систематические погрешности приборов, принимаются равными 0 2 — 0 5 цены наименьшего деления шкалы, если эта величина не превышает вариации показаний прибора. В ином случае максимальная абсолютная погрешность будет равна вариации показаний прибора, которая определяется при тарировании.
 

Вид кривой У 10 — 4Х2 и ее аппроксимация линейными отрезками.

Точность результата зависит от того, в каком состоянии находится счетчик-интегратор в момент остановки цикла вычисления. Для этого значения получаем максимальную абсолютную погрешность — 5 импульсов младшего разряда.
 

Например, при отсчете или установке визира на логарифмической линейке длиной 250 мм ошибка не превышает 0 1 мм. Таким образом, обычно бывает известна максимальная абсолютная погрешность, получаемая при измерении величины х; обозначим эту погрешность через их.
 

Оценка погрешности при прямых измерениях

При прямых измерениях искомая величина определяется непосредственно по отсчетному устройству (шкале) средства измерения. В общем случае измерения проводятся по определённому методу и при помощи некоторых средств измерений. Эти компоненты несовершенны и вносят свой вклад в погрешность измерения. Если тем или иным путём погрешность измерения (с конкретным знаком) удаётся найти, то она представляет собой поправку, которую просто исключают из результата. Однако достичь абсолютно точного результата измерения невозможно, и всегда остаётся некоторая «неопределённость», которую можно обозначить оценив границы погрешности. В России методики оценки погрешности при прямых измерениях стандартизированы ГОСТ Р 8.736-2011 и Р 50.2.038-2004.

В зависимости от имеющихся исходных данных и свойств оцениваемых погрешностей используют различные способы оценки. Случайная погрешность, как правило, подчиняется закону нормального распределения для описания которого необходимо указать математическое ожидание M{\displaystyle M} и среднеквадратическое отклонение σ.{\displaystyle \sigma .} В связи с тем, что при измерении проводится ограниченное число наблюдений, находят только наилучшие оценки этих величин: среднее арифметическое результатов наблюдений x¯{\displaystyle {\bar {x}}} и среднеквадратическое отклонение среднего арифметического Sx¯{\displaystyle S_{\bar {x}}}:

x¯=∑i=1nxin{\displaystyle {\bar {x}}={\frac {\sum _{i=1}^{n}x_{i}}{n}}}; Sx¯=∑i=1n(xi−x¯)2n(n−1).{\displaystyle S_{\bar {x}}={\sqrt {\frac {\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}}{n(n-1)}}}.}

Доверительные границы ε{\displaystyle \varepsilon } полученной таким образом оценки погрешности определяются умножением среднеквадратического отклонения на коэффициент Стьюдента t,{\displaystyle t,} выбранный для заданной доверительной вероятности P{\displaystyle P:}

ε=tSx¯.{\displaystyle \varepsilon =tS_{\bar {x}}.}

Систематические погрешности в силу своего определения не могут быть оценены путем проведения многократных измерений. Для составляющих систематической погрешности, обусловленной несовершенством средств измерений, как правило известны только их границы, представленные, например, основной погрешностью средства измерения.

Итоговая оценка границ погрешности получается суммированием вышеприведённых «элементарных» составляющих, которые рассматриваются как случайные величины. Эта задача может быть математически решена при известных функциях распределений этих случайных величин. Однако, в случае систематической погрешности, такая функция как правило неизвестна и форму распределения этой погрешности задают как равномерную. Основная трудность заключается в необходимости построения многомерного закона распределения суммы погрешностей, что практически невозможно уже при 3—4 составляющих. Поэтому используются приближённые формулы.

Суммарную неисключённую систематическую погрешность, когда она состоит из нескольких m{\displaystyle m} компонентов, определяют по следующим формулам:

Θ∑=±∑i=1m|Θi|{\displaystyle \Theta _{\sum }=\pm \sum _{i=1}^{m}\left|\Theta _{i}\right|} (если m<3{\displaystyle m<3});

Θ∑(P)=±∑i=1mΘi2{\displaystyle \Theta _{\sum }(P)=\pm {\sqrt {\sum _{i=1}^{m}\Theta _{i}^{2}}}} (если m⩾3{\displaystyle m\geqslant 3}),

где коэффициент k{\displaystyle k} для доверительной вероятности P=,95{\displaystyle P=0{,}95} равен 1,1.

Суммарная погрешность измерения, определяемая случайной и систематической составляющей, оценивается как:

Δ=KSx¯2+Θ∑23{\displaystyle \Delta =K{\sqrt {S_{\bar {x}}^{2}+{\frac {\Theta _{\sum }^{2}}{3}}}}} или Δ=KSx¯2+(Θ∑(P)k3)2{\displaystyle \Delta =K{\sqrt {S_{\bar {x}}^{2}+\left({\frac {\Theta _{\sum }(P)}{k{\sqrt {3}}}}\right)^{2}}}},

где K=ε+Θ∑Sx¯+Θ∑3{\displaystyle K={\frac {\varepsilon +\Theta _{\sum }}{S_{\bar {x}}+{\frac {\Theta _{\sum }}{\sqrt {3}}}}}} или K=ε+Θ∑(P)Sx¯+Θ∑(P)k3.{\displaystyle K={\frac {\varepsilon +\Theta _{\sum }(P)}{S_{\bar {x}}+{\frac {\Theta _{\sum }(P)}{k{\sqrt {3}}}}}}.}

Окончательный результат измерения записывается какA±Δ(P),{\displaystyle A\pm \Delta (P),} где A{\displaystyle A} — результат измерения (x¯,{\displaystyle {\bar {x}},}) Δ{\displaystyle \Delta } — доверительные границы суммарной погрешности, P{\displaystyle P} — доверительная вероятность.

Абсолютная погрешность — измерительный прибор

Абсолютная погрешность измерительного прибора представляет собой расхождение ( разность) между измеренным Ли и действительным ( истинным) Лд значениями измеряемой величины ДЛ — / 4н — Ац. Истинное значение измеряемой величины находят с учетом поправки. Поправка — это величина, обратная по знаку абсолютной погрешности: ДР — ДЛ Ал-А. Абсолютная погрешность электроизмерительных приборов со стрелочным показателем практически неизменна в пределах всей шкалы, поэтому с уменьшением значения измеряемой величины она возрастает. Для повышения точности измерения измеряемой величины на показывающих приборах со стрелочным указателем следует выбирать такие пределы измерения, чтобы отсчитывать показания примерно в пределах 2 / 3 всей шкалы.
 

Абсолютная погрешность измерительного прибора равна разности между показанием прибора и действительным ( точным) значением измеряемой величины.
 

Абсолютная погрешность измерительного прибора определяется разностью между показанием прибора и истинным значением измеряемой величины. Погрешность показаний прибора имеет своими источниками погрешности отдельных его элементов: чувствительного элемента, передаточного механизма и шкалы. Погрешность чувствительного элемента заключается в том, что действительная зависимость его перемещений от измеряемой величины не совпадает с расчетной, заложенной в схему прибора. Погрешность шкалы складывается из ошибки положения ее штрихов и эксцентриситета шкалы.
 

Абсолютной погрешностью измерительного прибора называется разность между его показанием и истинным значением измеряемой величины. Так как истинное значение измеряемой величины установить нельзя, в измерительной технике используется так называемое действительное значение, полученное с помощью образцового прибора.
 

Абсолютной погрешностью измерительного прибора называется разность между его показанием и истинным значением измеряемой величины. Поскольку последнее установить нельзя, то в измерительной технике используют так называемое действительное значение, полученное посредством образцового прибора.
 

Абсолютной погрешностью измерительного прибора называется разность между его показанием и истинным значением измеряемой величины Так как величину истинного значения измеряемой величины установить нельзя, в измерительной технике используется так называемое действительное значение, полученное с помощью образцового прибора.
 

Приведенная погрешность измерительного прибора — отношение абсолютной погрешности измерительного прибора к нормирующему значению, выраженное в процентах.
 

Корректность поставленных экспериментов доказана отсутствием превышения абсолютных ошибок измерения как при определении перемещений, так и напряжений над абсолютной погрешностью используемых измерительных приборов.
 

В некоторых случаях ( для образцовых и рабочих средств измерений повышенной точности) для исключения систематической погрешности показаний вводят поправку, равную абсолютной погрешности измерительного прибора.
 

Абсолютная погрешность измерительного прибора определяется разностью между показанием прибора и действительным значением измеряемой величины.
 

В данном разделе будут рассмотрены виды погрешностей, свойственные мерам, отдельным элементам и устройствам, а также средствам измерений в целом. Под абсолютной погрешностью меры понимают разность ( отклонение от номинального значения) между номинальным значением меры и истинным значением воспроизводимой ею величины. Так как истинное значение величины остается неизвестным, то на практике вместо него используют действительное значение величины. Следует различать абсолютную погрешность измерительного преобразователя по входу и по выходу. Абсолютную погрешность измерительного преобразователя по входу находят как разность между значением величины на входе преобразователя, определяемой в принципе по истинному значению величины на его выходе с помощью градуировочной характеристики, приписанной преобразователю, и истинным значением величины на входе преобразователя. Абсолютную погрешность измерительного преобразователя по выходу находят как разность между истинным значением величины на выходе преобразователя, отображающей измеряемую величину, и значением величины на выходе, определяемой в принципе по истинному значению величины на выходе с помощью градуировочной характеристики, приписанной преобразователю. Относительная погрешность измерительного прибора определяется как отношение абсолютной погрешности измерительного прибора к истинному значению измеряемой им величины.
 

Разрешение

Разрешением, или, как еще говорят, разрешающей способностью измерительной системы является наименьшая различимая измеряемая величина. Определение разрешения прибора не относится к точности измерения.

Цифровые измерительные системы

Цифровая система преобразует аналоговый сигнал в цифровой эквивалент посредством аналого-цифрового преобразователя. Разница между двумя значениями, то есть разрешение, всегда равно одному биту. Или, в случае с цифровым мультиметром, это одна цифра.

Возможно также выразить разрешение через другие единицы, а не биты. В качестве примера рассмотрим цифровой осциллограф, имеющий 8-битный АЦП. Чувствительность по вертикали установлена в 100 мВ/дел и число делений равно 8, полный диапазон, таким образом, равен 800 мВ. 8 бит представляются 28=256 различными значениями. Разрешение в вольтах тогда равно 800 мВ / 256 = 3125 мВ.

Аналоговые измерительные системы

В случае аналогового прибора, где измеряемая величина отображается механическим способом, как в стрелочном приборе, сложно получить точное число для разрешения. Во-первых, разрешение ограничено механическим гистерезисом, причиной которого является трение механизма стрелки. С другой стороны, разрешение определяется наблюдателем, делающем свою субъективную оценку.

Определение — погрешность — прибор

Схема поверки манометра МС-П.

Определение погрешности прибора производится при пяти значениях измеряемого давления. Измеряемое давление должно соответствовать определенной величине выходного сигнала.
 

Определение погрешности приборов 5 — й группы производится принципиально так же, как и для приборов 4 — й группы. Для понижения давления воздуха необходимо предусмотреть вентиль выпуска воздуха в атмосферу.
 

Определение погрешностей приборов классов 0 1; 0 2 и 0 5 производится при помощи компенсационного метода на потен-циометрических установках. Погрешности приборов классов 1 0; 1 5; 2 5 и 4 определяются путем сличения показаний их с показаниями образцовых стрелочных приборов.
 

Определение погрешности приборов классов точности 0 05; 0 1 и 0 2, пригодных для постоянного или для постоянного и переменного тока, производится при помощи компенсаторов. Приборы тех же классов точности, предназначенные только для переменного тока, поверяются термоэлектрическим методом компарирования. Этот метод заключается в замене измерения переменного тока измерением постоянного тока, равного по действующему значению переменному току. Равенство действующих значений постоянного и переменного тока устанавливается по неизменности термо — ЭДС термопреобразователя, являющегося основной частью компаратора.
 

Определение погрешностей приборов классов точности 0 05 — 0 5, пригодных для постоянного и переменного тока, должно производиться на постоянном и переменном токе.
 

Методика определения погрешности прибора приводится в его паспорте.
 

При определении погрешности At прибора в продольном направлении образцовую шкалу следует поместить на середину предметного стола так, чтобы ось ее делений была параллельна движению каретки продольного перемещения и чтобы направления возрастающих делений образцовой шкалы, и шкалы прибора, а также нулевые деления шкалы совпадали. Проверку нужно производить не менее трех раз в интервалах шкалы от 0 до 50, от 0 до 100, от 0 до 150 и от 0 до 200 мм; при проверке каждого интервала следует совместить изображения одной и той же пунктирной линии штриховой сетки визирной системы последовательно с изображениями нулевого и крайнего делений поверяемого интервала, соответственно каждый раз снимая отсчеты по шкале продольного перемещения.
 

При определении погрешности приборов высокой точности пользуются компенсационным методом. В этом случае действительное значение измеряемой величины определяется при помощи приборов сравнения — компенсаторов.
 

Рассмотренная методика определения погрешностей приборов позволяет оценить их точностные показатели при работе в идеальных статических условиях. Поэтому более объективной оценкой являются погрешности, полученные при проведении эксперимента на специальных стендах ( см. гл. Методика обработки результатов эксперимента по определению рассмотренных погрешностей аналогична описанной.
 

В целях определения погрешности прибора его поверяют. Процесс поверки в большинстве случаев состоит в сравнении показания поверяемого прибора с показанием более точного, образцового прибора при измерении ими одной и той же величины. Желая, например, поверить амперметр, включают его последовательно с образцовым амперметром и пропускают через них ток.
 

По этой причине определение погрешностей прибора при его испытаниях принято производить таким образом, чтобы можно было учесть влияние этих внешних факторов.
 

Упрощенная принципиальная схема потенциометрической установки.

Нагрузка в процессе определения погрешности прибора на одной из оцифрованных точек шкалы прибора остается постоянной, нестабильность выходной величины по нагрузке не будет являться определяющим параметром для ИП. Время влияния изменения выходной величины ИП на качество поверки по сравнению со временем дрейфа мало и исчисляется временем выполнения операции поверки на одной из оцифрованных отметок ( 0 5 — 1 мин), поэтому и дрейф выходной величины при выборе ИП может не приниматься в расчет.
 

Поверкой прибора называется процесс определения погрешности прибора.
 

Как найти погрешность измерения пример

Чтобы найти погрешность косвенных измерений, надо воспользоваться формулами, приведенными в таблице. Эти формулы могут быть выведены «методом границ».

Сначала надо вспомнить основные понятия теории погрешности.

Абсолютная погрешность физической величины ΔА — это разница между точным значением физической величины и ее приближенным значением и измеряется в тех же единицах, что и сама величина:

Так как мы никогда не знаем точного значения величины А, а лишь определяем из опыта ее приближенное значение, то и величину абсолютной погрешности мы можем определить лишь при­бли­зи­тель­но. Наиболее просто находится максимальная величина абсолютной погрешности, которая и используется нами в лабораторных работах.

Относительная погрешность измерения ε_А равна:

При косвенных измерениях величину погрешности искомой величины вычисляют по формулам:

В случае, когда искомая величина находится по формуле, в которой в основном присутствуют произведение и частное, удобней находить сначала относительную погрешность. Если при этом один из множителей представляет собой сумму или разность, нужно предварительно найти его абсолютную погрешность (сложением абсолютных погрешностей слагаемых), а затем относительную.

Зная относительную погрешность, найти абсолютную погрешность измерений можно так:

«Правило ничтожных погрешностей»

при суммировании погрешностей любым из слагаемых можно пренебречь, если оно не превосходит ⅓ – ⅟ 4 от другого.

Запись результата с указанием погрешности.

Абсолютная погрешность измерений обычно округляется до 1 значащей цифры, а, если эта цифра 1, то до двух.

Результат записывается в виде:

А = А_изм ± ΔА, например: ℓ = (13 ± 2) мм.

При этом в измеренном значении следует оставлять столько десятичных знаков, сколько их в значении погрешности (последняя цифра погрешности «поправляет» последнюю цифру измеренного значения) . Значение величины и погрешность следует выражать в одних и тех же единицах!

Пример оценки погрешностей косвенных измерений № 1

Пример оценки погрешностей косвенных измерений № 2

Задания для самостоятельного решения

Задание 1. Найдите плотность вещества, из которого сделан куб со стороной 7,00 ± 0,15 см, если его масса 847 ± 2 г. Что это за вещество?

Задание 2. Найдите удельную теплоту сгорания топлива, 2,10 ± 0,15 г которого хватило, чтобы нагреть 400 ± 10 мл воды на 35°С ± 2°С. Что это за топливо?

Ивашкина Д.А., 2017. Публикация материалов с сайта разрешена только при наличии активной ссылки на главную страницу.

Источник

По способу измерения[править | править код]

• Погрешность прямых измерений
• Погрешность косвенных измерений — погрешность вычисляемой (не измеряемой непосредственно) величины:

Если , где — непосредственно измеряемые независимые величины, имеющие погрешность , тогда:

Страница: 0

en: Observational error

de: Messabweichung

Примечанияправить | править код

1. РМГ 29-99 Рекомендации по межгосударственной сертификации. Основные термины и определения.
2. ISO/IEC Guide 2:2004. Standardization and related activities — General vocabulary
3. ГОСТ Р 50.2.038-2004 Измерения прямые однократные. Оценивание погрешностей и неопределенности результата измерений

Литератураправить | править код

• Назаров Н. Г. Метрология. Основные понятия и математические модели. М.: Высшая школа, 2002. 348 с.
• Лабораторные занятия по физике. Учебное пособие/Гольдин Л. Л., Игошин Ф. Ф., Козел С. М. и др.; под ред. Гольдина Л. Л. — М.: Наука. Главная редакция физико-математической литературы, 1983. — 704 с.

Для улучшения этой статьи желательно?:

Википедия Погрешность измерения адрес Викисловарь — адрес Викицитатник — адрес Викиучебник — адрес Викитека — адрес Викиновости — адрес Викиверситет — адрес Викигид — адрес

Выделить Погрешность измерения и найти в: Вокруг света измерения адрес Академик измерения/ru/ru/ адрес Астронет адрес Элементы измерения+&search адрес Научная Россия измерения&mode=2&sort=2 адрес Кругосвет измерения&results_per_page=10 адрес Научная Сеть Традиция — адрес Циклопедия — адрес Викизнание — измерения адрес

Bing Yahoo Яндекс Mail.ru Рамблер Нигма.РФ Спутник Google Scholar Апорт Архив Интернета Научно-популярные фильмы на Яндексе Документальные фильмы

Список ru-вики Вики-сайты на русском языке Список крупных русскоязычных википроектов Каталог wiki-сайтов Русскоязычные wiki-проекты Викизнание:Каталог wiki-сайтов Научно-популярные сайты в Интернете Лучшие научные сайты на нашем портале Лучшие научно-популярные сайты Каталог научно-познавательных сайтов НАУКА В РУНЕТЕ: каталог научных и научно-популярных сайтов

• Страница — краткая статья
• Страница — энциклопедическая статья
• Разное — на страницах: , , ,

Как определить класс точности электроизмерительного прибора, формулы расчета

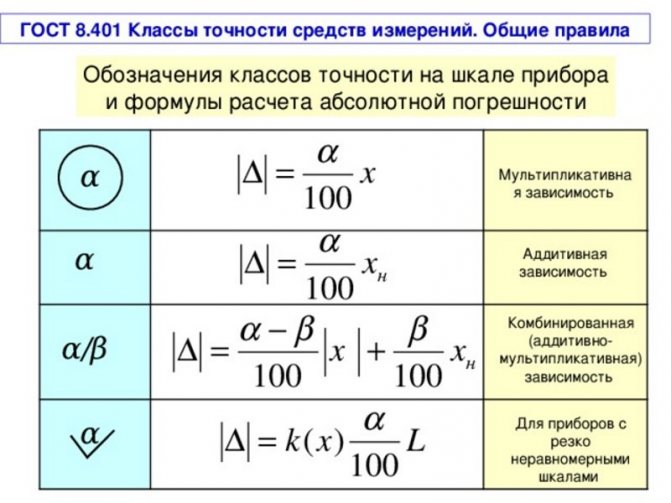
Чтобы определить класс точности, необходимо взглянуть на его корпус или инструкцию пользователя, в ней вы можете увидеть цифру, обведенную в круг, например, ① это означает, что ваш прибор измеряет величину с относительной погрешностью ±1%.

Но что делать если известна относительная погрешность и необходимо рассчитать класс точности, например, амперметра, вольтметра и т.д. Рассмотрим на примере амперметра: известна ∆x=базовая (абсолютная) погрешность 0,025 (см. в инструкции), количество делений х=12

Находим относительную погрешность:

Y= 100×0,025/12=0,208 или 2,08%

(вывод: класс точности – 2,5).

Следует отметить, что погрешность неравномерна на всем диапазоне шкалы, измеряя малую величину вы можете получить наибольшую неточность и с увеличением искомой величины она уменьшается, для примера рассмотрим следующий вариант:

Вольтметр с классом p=±2, верхний предел показаний прибора Xn=80В, число делений x=12

Предел абсолютной допустимой погрешности:

Относительная погрешность одного деления:

Если вам необходимо выполнить более подробный расчет, смотрите ГОСТ 8.401-80 п.3.2.6.

Что такое класс точности

Сам по себе класс не является постоянной величиной измерения, потому что само измерение зачастую зависит от множества переменных: места измерения, температуры, влажности и других факторов, класс позволяет определить лишь только в каком диапазоне относительных погрешностей работает данный прибор.

Чтобы заранее оценить погрешность, которую измерит устройство, также могут использоваться нормативные справочные значения.

Устаревание, несовершенство изготовления измерителей, внешние воздействия — это основной показатель отклонения погрешностей.

Относительная погрешность — это отношение абсолютной погрешности к модулю действительного приближенного показателя полученного значения, измеряется в %.

Абсолютная погрешность рассчитывается следующим образом:

∆=±a или ∆=(a+bx)

x – число делений, нормирующее значение величины

a, b – положительные числа, не зависящие от х

Абсолютная и приведенная погрешность рассчитывается по следующим формулам, см. таблицу ниже

По причине возникновения[править | править код]

• Методические погрешности — погрешности, обусловленные несовершенством метода, а также упрощениями, положенными в основу методики.
• Субъективные / операторные / личные погрешности — погрешности, обусловленные степенью внимательности, сосредоточенности, подготовленности и другими качествами оператора.

Если прибор работает в условиях, отличных от нормальных, то возникает дополнительная погрешность, увеличивающая общую погрешность прибора. К дополнительным погрешностям относятся: температурная, вызванная отклонением температуры окружающей среды от нормальной, установочная, обусловленная отклонением положения прибора от нормального рабочего положения, и т. п. За нормальную температуру окружающего воздуха принимают 20 °C, за нормальное атмосферное давление 101,325 кПа.

Обобщенной характеристикой средств измерения является класс точности, определяемый предельными значениями допускаемых основной и дополнительной погрешностей, а также другими параметрами, влияющими на точность средств измерения; значение параметров установлено
стандартами на отдельные виды средств измерений. Класс точности средств измерений характеризует их точностные свойства, но не является непосредственным показателем точности измерений, выполняемых с помощью этих средств, так как точность зависит также от метода измерений и условий их выполнения. Измерительным приборам, пределы допускаемой основной погрешности которых заданы в виде приведенных основных (относительных) погрешностей, присваивают классы точности, выбираемые из ряда следующих чисел: (1; 1,5; 2,0; 2,5; 3,0; 4,0; 5,0; 6,0)*10n, где показатель степени n = 1; 0; −1; −2 и т. д.

Учимся определять погрешность взвешивания

Это один из примеров прямых измерений. На особом месте стоит взвешивание. Ведь у рычажных весов нет шкалы. Научимся определять погрешность такого процесса. На точность измерения массы влияет точность гирь и совершенство самих весов.

Мы пользуемся рычажными весами с набором гирь, которые необходимо класть именно на правую чашу весов. Для взвешивания возьмем линейку.

Перед началом опыта нужно уравновесить весы. Линейку кладем на левую чашу.

Масса будет равна сумме установленных гирь. Определим погрешность измерения этой величины.

D m = D m (весов) + D m (гирь)

Погрешность измерения массы складывается из двух слагаемых, связанных с весами и гирями. Чтобы узнать каждую из этих величин, на заводах по выпуску весов и гирь продукция снабжается специальными документами, которые позволяют вычислить точность.

Поверка приборов, для чего она нужна

Все измерительные приборы измеряют с некой погрешностью, класс точности говорит лишь о том, в каком диапазоне она находится. Бывают случаи, когда диапазон погрешности незаметно увеличивается, и мы начинаем замечать, что измеритель «по-простому» начинает врать. В таких случаях помогает поверка.

Это процесс измерения эталонной величины в идеальных условиях прибором, обычно проводится метрологической службой или в метрологическом отделе предприятия производителя.

Существует первичная и периодическая, первичную проверку проводят после выпуска изделия и выдают сертификат, периодическую проводят не реже чем раз в год, для ответственных приборов чаще.

Поэтому если вы сомневаетесь в правильности работы устройства, вам следует провести его поверку в ближайшей метрологической службе, потому что измеритель может врать как в меньшую, так и в большую сторону.

Как легко проверить потребление электроэнергии в квартире, можете узнать в нашей статье.