Погрешность измерения

Введение

Все, что сказано в этом введении, запоминать не нужно. это справочный материал, к которому вы будете обращаться при выполнении лабораторных работ.

1. Как определять погрешности измерений

Выполнение лабораторных работ связано с измерением различных физических величин и последующей обработкой их результатов.

Измерение — нахождение значения физической величины опытным путем с помощью средств измерений.

Прямое измерение — определение значения физической величины непосредственно средствами измерения.

Косвенное измерение — определение значения физической величины по формуле, связывающей ее с другими физическими величинами, определяемыми прямыми измерениями.

Введем следующие обозначения:

A, B, C, … — физические величины.

A_пр — приближенное значение физической величины, т.е. значение, полученное путем прямых или косвенных измерений.

ΔA — абсолютная погрешность измерения физической величины.

ε — относительная погрешность измерения физической величины, равная:

Δ_иA — абсолютная инструментальная погрешность, определяемая конструкцией прибора (погрешность средств измерения; указывается в каждой работе при описании прибора в разделе Оборудование и средства измерения)

Δ_оA — абсолютная погрешность отсчета (получающаяся от недостаточно точного отсчета показаний средств измерения), она равна в большинстве случаев половине цены деления; при измерении времени — цене деления секундомера или часов.

Максимальная абсолютная погрешность прямых измерений складывается из абсолютной инструментальной погрешности и абсолютной погрешности отсчета при отсутствии других погрешностей:

ΔA=Δ_иA + Δ_оA

Абсолютную погрешность измерения обычно округляют до одной значащей цифры (ΔA≈0,17=0,2); численное значение результата измерений округляют так, чтобы его последняя цифра оказалась в том же разряде, что и цифра погрешности (А=10,332≈10,3).

Результаты повторных измерений физической величины А, проведенных при одних и тех же контролируемых условиях и при использовании достаточно чувствительных и точных (с малыми погрешностями) средств измерения, отличаются друг от друга.

В этом случае A_пр находят как среднее арифметическое значение всех измерений, а ΔA (ее в этом случае называют случайной погрешностью) определяют методами математической статистики.

В школьной лабораторной практике такие средства измерения практически не используются. Поэтому при выполнении лабораторных работ необходимо определять максимальные погрешности измерения физических величин. При этом для получения результата достаточно одного измерения.

Относительная погрешность косвенных измерений определяется, как показано в таблице 1.

Абсолютная погрешность косвенных измерений определяется по формуле ΔA=A_прε (ε выражается десятичной дробью).

Таблица 1

Формулы для нахождения относительной погрешности косвенных измерений

Nº п/п	Формула физической величины	Формула относительной погрешности
1
2
3	A=B+C
4

2. О классе точности электроизмерительных приборов

Для определения абсолютной инструментальной погрешности прибора надо знать его класс точности. Класс точности γ_пр измерительного прибора показывает, сколько процентов составляет абсолютная инструментальная погрешность Δ_иA от всей шкалы прибора (A_max):

Класс точности указывается при описании прибора в разделе Оборудование и средства измерения. Cуществуют следующие классы точности электроизмерительных приборов: 0,1; 0,2; 0,5; 1; 1,5; 2,5; 4. Зная класс точности прибора (γ_пр) и всю его шкалу (A_max), определяют абсолютную погрешность Δ_иA измерения физической величины А этим прибором:

3. Как сравнивать результаты измерений

1. Записать результаты измерений в виде двойных неравенств:

A_{1 пр} – ΔA₁ < A_{1 пр} < A_{1 пр} + ΔA₁
A_{2 пр} – ΔA₂ < A_{2 пр} < A_{2 пр} + ΔA₂
2. Сравнить полученные интервалы значений (рис.1): если интервалы не перекрываются, то результаты неодинаковы, если перекрываются — одинаковы при данной относительной погрешности измерений.

Рисунок 1.

4. Как оформлять отчет о проделанной работе

Отчетом о проделанной работе является форма, находящаяся в левом нижнем окне. После ее заполнения надо нажать на кнопку «Отправить результаты на сервер».

Значения измеренных физических величин переносятся в таблицу результатов автоматически после нажатия соответствующей кнопки.

Значения остальных величин и ответ на контрольный вопрос вводятся с клавиатуры.

домашней странице BARSIC

Вычисление погрешности измерений

Школьникам и студентам, выполняющим лабораторные работы, чаще всего приходится вычислять абсолютные и относительные погрешности. Делается это при помощи некоторого набора формул и определений.

Абсолютная погрешность ΔА вычисляется как разность между истинным значением величины (А) и ее приблизительным значением (Апр):

ΔА = А — Апр.

Относительная погрешность δА вычисляется как выраженное в процентах отношение абсолютной погрешности ΔА к приблизительному значению Апр:

δА = (ΔА / Апр) • 100%.

Абсолютная инструментальная погрешность ΔиА зависит от конструкции конкретного измерительного прибора и от его класса точности. Обычно это значение указывается на шкале прибора или в его паспорте.

С помощью класса точности можно рассчитать инструментальную погрешность ΔиА, выраженную в процентах. Для этого значение класса точности нужно умножить на наибольшее значение, которое способен измерять данный прибор, и поделить результат на 100.

То есть класс точности (обозначим его γ) связан с абсолютной инструментальной погрешностью (ΔиА) и максимальным показанием шкалы (Аmax) следующей формулой:

γ = ΔиА / Аmax • 100%.

Величины класса точности (γ) и максимально возможного показания шкалы (Аmax) можно узнать из паспорта прибора, которым будет производиться измерение. На их основе можно рассчитать абсолютную погрешность, с которой будет произведено измерение:

ΔиА = γ • Аmax / 100.

Поясним это на примере

Пусть амперметр имеет шкалу от 0 до 5 А, и на его шкале указан класс точности 0,5. Тогда инструментальная погрешность измерений при помощи такого амперметра будет:

ΔиА = 0,5 • 5 / 100 = 0,025.

Часто бывает так, что класс точности не указывают. В этом случае абсолютная инструментальная погрешность принимается такой же, как и погрешность отсчета ΔоА, которая принимается равной половине цены деления шкалы измерительного прибора.

Например, погрешность отсчета у обычной школьной линейки с миллиметровыми делениями принимается равной 0,5 мм. Если же линейка проградуирована не в миллиметрах, а, скажем, в дюймах, то погрешность отсчета ΔоА будет равна 0,5 дюймов.

Одна и та же величина, измеренная разными инструментами, будет иметь разную ошибку, и даже разное значение, так как результат необходимо округлять с той точностью, которую обеспечивает конкретная линейка.

Например, вот какие результаты мы получаем при измерении отрезка длиной 7 дюймов сначала при помощи дюймовой линейки, а затем при помощи двухдюймовой линейки.

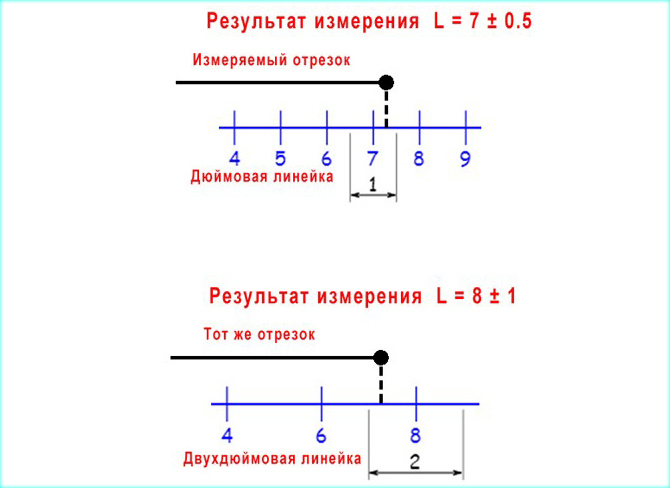
Также точность конечного результата будет зависеть и от условий, в которых проводится измерение.

Рассмотрим решение следующей простой задачи: 25 зубочисток плотно лежат в коробочке. Ширину коробочки измерили обычной линейкой и получили значение 30 мм. Чему равна толщина одной зубочистки (толщиной стенок коробочки можно пренебречь)?

Решение:

Линейка обеспечивает погрешность измерений 0,5 мм.

Толщина одной зубочистки:

l = 30 / 25 = 1,2 мм.

Погрешность измерения толщины 25 зубочисток будет 0,5 мм, значит погрешность измерения толщины одной зубочистки:

Δl = 0,5 / 25 = 0,02.

Согласно правилам в ответе мы должны привести определяемую величину с той же точностью, что и ее погрешность. Таким образом, получаем следующий ответ.

Ответ:

l = 1,20 ± 0,02 мм.

Если же инструментальная погрешность ΔиА прибора известна, то максимальная абсолютная погрешность произведенных с его помощью измерений будет равна сумме абсолютной погрешности измерений и абсолютной инструментальной. Она рассчитывается по формуле:

ΔА = ΔоА + ΔиА.

При расчетах абсолютную погрешность принято округлять до одной значащей цифры.

Приведенная относительная погрешность

Приведенная относительная погрешность прибора — это погрешность, выраженная в процентах от его предела измерения. Ее вычисляют или от суммы верхнего и нижнего пределов измерения, если прибор имеет двухстороннюю шкалу измерения ( с нулевой отметкой в середине шкалы), или от разности пределов при односторонней шкале.
 

Наибольшая основная приведенная относительная погрешность, выраженная в процентах, характеризует класс точности прибора.
 

Приведенную относительную погрешность для приборов со шкалой, начинающейся от нулевого значения измеряемой величины, определяют в процентах от верхнего предела измерения, для приборов с безнулевой шкалой — от среднего арифметического пределов измерения, а для приборов с двусторонней шкалой — от суммы пределов измерения.
 

Приведенной относительной погрешностью называется отношение абсолютной погрешности к максимальному значению выходной величины, определяющему диапазон ее изменения.
 

При постоянной приведенной относительной погрешности прибора относительная погрешность измерения возрастает с уменьшением измеряемой величины.
 

Допустимая величина приведенной относительной погрешности едол определяет класс точности прибора, указываемый на его шкале. По ГОСТ 1845 — 59 предусматриваются следующие классы точности электроизмерительных приборов: 0 05; 0 1; 0 2; 0 5; 1 0; 1 5; 2 5; 4 0 и классы 0 02; 0 05; 0 1; 0 2; 0 5; 1 0 для шунтов и добавочных сопротивлений к приборам.
 

Используется также оценка приведенной относительной погрешности ( отн.
 

Прибор с зеркальной шкалой. / — шкала. 2 -стрелка. Л — зеркало.| Нопиуеиая шкала.

Завод-изготовитель гарантирует, что наибольшая приведенная относительная погрешность прибора в пределах рабочей части его шкалы не превышает определенного значения, называемого допустимой п о г р е ш-н о с т ь ю прибора.
 

При постоянстве абсолютной погрешности Ду приведенная относительная погрешность b также постоянна.
 

Приборы класса 0 1 ( допустимая приведенная относительная погрешность 0 1 %), как правило, являются лабораторными.
 

Класс точности прибора характеризуется величиной приведенной относительной погрешности. Большинство радиоизмерительных приборов на классы не делят, так как применяемые стрелочные индикаторы используют совместно с соответствующей электронной схемой.
 

Схема опре деления погрешности.

Обычно для оценки точности элементов используется приведенная относительная погрешность.
 

При постоянстве абсолютной погрешности Дг / приведенная относительная погрешность b также постоянна.
 

Правила подсчета погрешностей

Для номинальной оценки погрешностей существует несколько правил:

• при сложении и вычитании чисел необходимо складывать их абсолютные погрешности;
• при делении и умножении чисел требуется сложить относительные погрешности;
• при возведении в степень относительную погрешность умножают на показатель степени.

Приближенные и точные числа записываются при помощи десятичных дробей. Берется только среднее значение, поскольку точное может быть бесконечно длинным. Чтобы понять, как записывать эти числа, необходимо узнать о верных и сомнительных цифрах.

Верными называются такие цифры, разряд которых превосходит абсолютную погрешность числа. Если же разряд цифры меньше абсолютной погрешности, она называется сомнительной. Например, для дроби 3,6714 с погрешностью 0,002 верными будут цифры 3,6,7, а сомнительными – 1 и 4. В записи приближенного числа оставляют только верные цифры. Дробь в этом случае будет выглядеть таким образом – 3,67.

Что мы узнали?

Абсолютные и относительные погрешности используются для оценки точности измерений. Абсолютной погрешностью называют разницу между точным и приближенным числом. Относительная погрешность – это отношение абсолютной погрешности числа к самому числу. На практике используют относительную погрешность, так как она является более точной.

Тест по теме

1. Вопрос 1 из 10

Начать тест(новая вкладка)

Абсолютная и относительная погрешность

Абсолютной погрешностью или, короче, погрешностью приближенного
числа называется разность между этим числом и его точным значением (из большего числа вычитается меньшее)*.

Пример 1. На предприятии 1284 рабочих и служащих. При
округлении этого числа до 1300 абсолютная погрешность
составляет 1300 — 1284 = 16. При округлении до 1280 абсолютная погрешность составляет 1284 — 1280 = 4.

Относительной погрешностью приближенного числа называется отношение
абсолютной погрешности приближенного числа к самому этому числу.

Пример 2. В школе 197 учащихся. Округляем это число до 200. Абсолютная
погрешность составляет 200 — 197 = 3. Относительная погрешность равна 3/197 или, округленно, 3/197 = 1,5 %.

В большинстве случаев невозможно узнать точное значение приближенного числа, а значит, и точную величину погрешности.
Однако почти всегда можно установить, что погрешность (абсолютная или относительная) не превосходит некоторого числа.

Пример 3. Продавец взвешивает арбуз на чашечных весах. В наборе гирь наименьшая — 50 г. Взвешивание дало 3600 г. Это число – приближенное. Точный вес арбуза
неизвестен. Но абсолютная погрешность не
превышает 50 г. Относительная погрешность не превосходит 50/3600 ≈ 1,4%.

Число, заведомо превышающее абсолютную погрешность (или в худшем случае равное ей), называется предельной абсолютной погрешностью. Число, заведомо превышающее
относительную погрешность (или в худшем случае равное ей), называется предельной относительной погрешностью.

В примере 3 за предельную абсолютную погрешность можно взять 50 г, а за предельную относительную погрешность — 1,4 %.

Величина предельной погрешности не является вполне определенной. Так, в примере 3 можно принять за предельную абсолютную
погрешность 100 г, 150 г и вообще всякое число, большее чем 50 г. На практике берется по возможности меньшее значение
предельной погрешности. В тех случаях, когда известна точная величина погрешности, эта величина служит одновременно
предельной погрешностью. Для каждого приближенного числа должна быть известна его предельная погрешность
(абсолютная или oотносительная). Когда она прямо не указана, подразумевается что предельная абсолютная погрешность
составляет половину единицы последнего выписанного разряда. Так, если приведено приближенное число 4,78 без указания
предельной погрешности, то подразумевается, что предельная абсолютная погрешность составляет 0,005. Вследствие этого
соглашения всегда можно обойтись без указания предельной погрешности числа.

Предельная абсолютная погрешность обозначается греческой буквой Δ («дельта»); предельная относительная
погрешность — греческой буквой δ («дельта малая»). Если приближенное число обозначить буквой а, то

δ = Δ/a.

Пример 4. Длина карандаша измерена линейкой с миллиметровыми делениями. Измерение показало 17,9 см. Какова предельная
относительная погрешность этого измерения?
Здесь а = 17,9 см; можно принять Δ = 0,1 см, так как с точностью до 1 мм измерить карандаш нетрудно, a значительно уменьшить, предельную погрешность ни удастся (при навыке можно прочесть на хорошей линейке и 0,02 и даже 0,01 см, но у самого карандаша ребра могут разниться на бoльшую величину). Относительная погрешность равна 0,1/17,9.
Округляя, находим δ = 0,1/18 ≈ 0,6%.

Пример 5. Цилиндрический поршень имеет около 35 мм в диаметре. С какой точностью нужно его измерить микрометром, чтобы
предельная относительная погрешность составляла 0,05%?Решение. По условию, предельная абсолютная погрешность должна составлять 0,05% от 35 мм. Следовательно, предельная
абсолютная погрешность равна 36*(0,05/100) = 0,0175 (мм) или, усиливая, 0,02 (мм). Можно воспользоваться
формулой δ = Δ/a.
Подставляя в неё а = 35, δ = 0,0005, имеем 0,0005 = Δ/35. Значит, Δ = 35 • 0,0005 = 0,0175 (мм).

* Иначе говоря, если a есть приближенное число, а х – его точное значение, то абсолютная погрешность есть абсолютное
значение разности a – х. В некоторых руководствах абсолютной погрешностью называется сама
разность a – х (или разность х — a). Эта величина может быть положительной или отрицательной.

Советы по выбору счетчиков

Выбор приборов учета в магазинах — достаточно большой.

Анализируя, какой счетчик электроэнергии лучше, рекомендуется обратить внимание на следующие аспекты:

• стоимость счетчика (но нельзя кидаться на слишком дешевую продукцию, так как при ее изготовлении могли применяться низкокачественные комплектующие, снижающие срок службы оборудования);
• производителя устройства, сделав выбор в пользу проверенных компаний;
• гарантийный срок прибора;
• потребление электроэнергии самими счетчиками;
• уровень шума прибора;
• возможность осуществлять сервисное обслуживание.

Не нужно сразу отказываться от покупки немного морально устаревших индукционных моделей. Они, как и электронные приборы, имеют свои преимущества. Нет необходимости также приобретать устройства, имеющие множество функций, которые не будут использоваться. К тому же большое количество микросхем в счетчиках повышает риск его выхода из строя.

Паспорт на электросчетчик

Важно тщательно проверить дату проведенной поверки счетчика. Согласно ПУЭ вновь устанавливаемые приборы должны иметь пломбы госповерки с давностью:

Согласно ПУЭ вновь устанавливаемые приборы должны иметь пломбы госповерки с давностью:

• для трехфазных моделей: до одного года;
• для однофазных: до двух лет.

Таким образом, если дата поверки истекла, прибор не поставят на учет без проведения новой.

Помимо известных зарубежных производителей, продукция которых давно пользуется популярностью (ABB, GE) на рынке представлены и модели отечественных компаний (Энергомера — производитель одноименных приборов, Инкотекс, выпускающий счетчики Меркурий, Тайпит, предлагающий регистраторы Нева). Причем, их качество порой не уступает импортным, а цена — гораздо ниже.

Технические характеристики

Согласно документации, на схемах сети вольтметры принято обозначение окружностью с вписанной латинской буквой «V». На русских смехах он может заменяться на русскую букву «В». Более того, первая цифра после буквы в маркировке отображает тип устройства и специфику его использования. Например, В2 — вольтметр для постоянного тока, В3 — для переменного, В4 — для импульсного и т.д.

Вам это будет интересно Разновидности бытовых и промышленных электрических выключателей

Аппарат В3-38 для использования в сетях переменного тока

Оценка характеристик прибора включает в себя следующие компоненты:

• Диапазон измерений. Он ограничивается наименьшим и наибольшим показателем, который способен изменить аппарат. Современные устройства обладают диапазоном от милливольт до киловольт. Промышленные аналоги же способны измерять как меньшие, так и большие напряжения;
• Точность измерений. Далеко не каждый домашний тестер отличается повышенной точностью измерений. Как уже было сказано, это зависит от его внутреннего сопротивления. Новые вольтметры при сравнительно небольших размерах обладают маленькими погрешностями измерений;
• Диапазон частот. Показывает чувствительность прибора к тем или иным сигналам с разными частотами, регистрируемых в сети;
• Температура и другие факторы. Эти параметры определяют показатели, при которых аппарат обладает минимальной погрешностью измерений, доступной для него;
• Собственно само внутреннее сопротивление (импеданс). Чем выше этот параметр, тем вольтметр более точен.

Цифровые устройства практически полностью вытеснили аналоговые

Важно! Технические характеристики аналоговых приборов сильно зависят от чувствительности магнитоэлектрического прибора. Чем меньше его ток полного отклонения, тем более высокосопротивительные резисторы можно использовать

ВЕСА РЕЗУЛЬТАТОВ НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ

При неравноточных измерениях, когда результаты каждого измерения нельзя считать одинаково надежными, уже нельзя обойтись определением простого арифметического среднего. В таких случаях учитывают достоинство (или надежность) каждого результата измерений.Достоинство результатов измерений выражают некоторым числом, называемым весом этого измерения. Очевидно, что арифметическое среднее будет иметь больший вес по сравнению с единичным измерением, а измерения, выполненные при использовании более совершенного и точного прибора, будут иметь большую степень доверия, чем те же измерения, выполненные прибором менее точным.
Поскольку условия измерений определяют различную величину средней квадратической погрешности, то последнюю и принято принимать в качестве основы оценки весовых значений, проводимых измерений. При этом веса результатов измерений принимают обратно пропорциональными квадратам соответствующих им средних квадратических погрешностей.
Так, если обозначить через р и Р веса измерений, имеющие средние квадратические погрешности соответственно m и µ, то можно записать соотношение пропорциональности:

Например, если µ средняя квадратическая погрешность арифметического среднего, а m – соответственно, одного измерения, то, как следует из

можно записать:

т. е. вес арифметического среднего в n раз больше веса единичного измерения.

Аналогичным образом можно установить, что вес углового измерения, выполненного 15-секундным теодолитом, в четыре раза выше веса углового измерения, выполненного 30-секундным прибором.

При практических вычислениях обычно вес одной какой-либо величины принимают за единицу и при этом условии вычисляют веса остальных измерений. Так, в последнем примере если принять вес результата углового измерения 30-секундным теодолитом за р = 1, то весовое значение результата измерения 15-секундным теодолитом составит Р = 4.

Абсолютная погрешность — измерительный прибор

Абсолютная погрешность измерительного прибора представляет собой расхождение ( разность) между измеренным Ли и действительным ( истинным) Лд значениями измеряемой величины ДЛ — / 4н — Ац. Истинное значение измеряемой величины находят с учетом поправки. Поправка — это величина, обратная по знаку абсолютной погрешности: ДР — ДЛ Ал-А. Абсолютная погрешность электроизмерительных приборов со стрелочным показателем практически неизменна в пределах всей шкалы, поэтому с уменьшением значения измеряемой величины она возрастает. Для повышения точности измерения измеряемой величины на показывающих приборах со стрелочным указателем следует выбирать такие пределы измерения, чтобы отсчитывать показания примерно в пределах 2 / 3 всей шкалы.
 

Абсолютная погрешность измерительного прибора равна разности между показанием прибора и действительным ( точным) значением измеряемой величины.
 

Абсолютная погрешность измерительного прибора определяется разностью между показанием прибора и истинным значением измеряемой величины. Погрешность показаний прибора имеет своими источниками погрешности отдельных его элементов: чувствительного элемента, передаточного механизма и шкалы. Погрешность чувствительного элемента заключается в том, что действительная зависимость его перемещений от измеряемой величины не совпадает с расчетной, заложенной в схему прибора. Погрешность шкалы складывается из ошибки положения ее штрихов и эксцентриситета шкалы.
 

Абсолютной погрешностью измерительного прибора называется разность между его показанием и истинным значением измеряемой величины. Так как истинное значение измеряемой величины установить нельзя, в измерительной технике используется так называемое действительное значение, полученное с помощью образцового прибора.
 

Абсолютной погрешностью измерительного прибора называется разность между его показанием и истинным значением измеряемой величины. Поскольку последнее установить нельзя, то в измерительной технике используют так называемое действительное значение, полученное посредством образцового прибора.
 

Абсолютной погрешностью измерительного прибора называется разность между его показанием и истинным значением измеряемой величины Так как величину истинного значения измеряемой величины установить нельзя, в измерительной технике используется так называемое действительное значение, полученное с помощью образцового прибора.
 

Приведенная погрешность измерительного прибора — отношение абсолютной погрешности измерительного прибора к нормирующему значению, выраженное в процентах.
 

Корректность поставленных экспериментов доказана отсутствием превышения абсолютных ошибок измерения как при определении перемещений, так и напряжений над абсолютной погрешностью используемых измерительных приборов.
 

В некоторых случаях ( для образцовых и рабочих средств измерений повышенной точности) для исключения систематической погрешности показаний вводят поправку, равную абсолютной погрешности измерительного прибора.
 

Абсолютная погрешность измерительного прибора определяется разностью между показанием прибора и действительным значением измеряемой величины.
 

В данном разделе будут рассмотрены виды погрешностей, свойственные мерам, отдельным элементам и устройствам, а также средствам измерений в целом. Под абсолютной погрешностью меры понимают разность ( отклонение от номинального значения) между номинальным значением меры и истинным значением воспроизводимой ею величины. Так как истинное значение величины остается неизвестным, то на практике вместо него используют действительное значение величины. Следует различать абсолютную погрешность измерительного преобразователя по входу и по выходу. Абсолютную погрешность измерительного преобразователя по входу находят как разность между значением величины на входе преобразователя, определяемой в принципе по истинному значению величины на его выходе с помощью градуировочной характеристики, приписанной преобразователю, и истинным значением величины на входе преобразователя. Абсолютную погрешность измерительного преобразователя по выходу находят как разность между истинным значением величины на выходе преобразователя, отображающей измеряемую величину, и значением величины на выходе, определяемой в принципе по истинному значению величины на выходе с помощью градуировочной характеристики, приписанной преобразователю. Относительная погрешность измерительного прибора определяется как отношение абсолютной погрешности измерительного прибора к истинному значению измеряемой им величины.
 

Электростатические КИП

Эти приборы работают на принципе взаимодействия заряженных электродов, которые разделены диэлектриком. Конструктивно они выглядят практически как плоский конденсатор. При этом, при перемещении подвижной части емкость системы также изменяется.

Наиболее известные из них – это устройства с линейным и поверхностным механизмом. У них немного разный принцип действия. У приборов с поверхностным механизмом емкость изменяется за счет колебаний активной площади электродов

В другом случае важно расстояние между ними

К достоинствам таких устройств относятся небольшая мощность потребления, класс точности ГОСТ, достаточно широкий частотный диапазон и т.д.

Недостатками являются небольшая чувствительность прибора, необходимость экранирования и пробой между электродами.

Максимальная абсолютная погрешность

Процесс зфавновсшивагия в цифровых приборах развертывающего уравновеши.

В цифровых циклических приборах выходной код N приближается к искомому отсчету Nх с одной стороны, сверху или снизу, поэтому при АХп ч 0 максимальная абсолютная погрешность от квантования равна ступени & хк.
 

Здесь: Арн — максимальная абсолютная погрешность величины рн, равная половине единицы разряда последней значащей цифры в табличном значении рн; Ар и АГ — максимальные абсолютные погрешности измерения р и Т соответственно.
 

Абсолютная погрешность температурного предела смеси при использовании в расчете надежных экспериментальных данных по давлению пара чистых компонентов, растворимости и коэффициентам активности, как правило, не превышает максимальной абсолютной погрешности температурного предела компонентов смеси.
 

Абсолютная погрешность при изображении в ячейке чисел с запятой, фиксированной после определенного разряда, не превосходит по величине единицы младшего разряда, то есть, как говорят, максимальная абсолютная погрешность при этом постоянна. https://spb-evacuator.ru.
 

Для учета в модели однократной экстракции NRTL влияния воды, были дополнительно подобраны эмпирические коэффициенты бинарного взаимодействия воды с компонентами системы, применение которых при численных исследованиях существенно уменьшило погрешности моделирования в области содержания воды в экстрагенте выше 8 % об. По выходу рафината и содержанию в нем аренов максимальные абсолютные погрешности в этой области составляют 0 6 и 0 9 %, соответственно. Погрешности расчета по выходу экстракта и содержания в нем аренов снизились до 0 6 и 1 1 %, что составляет 4 8 и 1 4 % относительной по.
 

Следует отметить, что для измерения среднего фазового сдвига рассмотренным методом характерно уменьшение погрешности дискретности по сравнению с имеющей место при измерении одиночного интервала времени. Хотя максимальная абсолютная погрешность дискретности определения длительности одного интервала АГ составляет ГСЧ, результирующая погрешность за время измерения Ткзм уменьшается, так как результаты измерения всех k интервалов АГ суммируются, а возникновение частотной погрешности дискретности положительного или отрицательного знака равновероятно.
 

Рассмотрим погрешность от квантования. Следовательно, максимальная абсолютная погрешность от квантования будет равна единице.
 

Второй способ сводится к увеличению числа импульсов, заполняющих временные ворота, достигаемому умножением частоты исследуемого сигнала. При этом максимальная абсолютная погрешность меняется ( если неизменна длительность ворот), но уменьшается относительная погрешность. Осуществление данного способа сопряжено с применением дополнительного блока — умножителя частоты, что усложняет и удорожает аппаратуру.
 

Максимальную погрешность Дгд Т0 удобно учитывать через эквивалентное случайное изменение числа счетных импульсов Nx на 1 импульс. При этом максимальная абсолютная погрешность дискретизации может быть определена разностью значений частоты / получаемых по формулам (7.4) или (7.5) при Л 1 и Nx, и равна А.
 

Максимальные абсолютные погрешности показаний манометров Мп и Мв, исправленных на систематические погрешности приборов, принимаются равными 0 2н — 0 5 цены наименьшего деления шкалы, если эта величина не превышает вариации показаний прибора. В противном случае максимальная абсолютная погрешность равна вариации показа ний прибора, которая определяется при тарировании.
 

Максимальные абсолютные погрешности показаний манометров М и Мв, исправленных на систематические погрешности приборов, принимаются равными 0 2 — 0 5 цены наименьшего деления шкалы, если эта величина не превышает вариации показаний прибора. В ином случае максимальная абсолютная погрешность будет равна вариации показаний прибора, которая определяется при тарировании.
 

Вид кривой У 10 — 4Х2 и ее аппроксимация линейными отрезками.

Точность результата зависит от того, в каком состоянии находится счетчик-интегратор в момент остановки цикла вычисления. Для этого значения получаем максимальную абсолютную погрешность — 5 импульсов младшего разряда.
 

Например, при отсчете или установке визира на логарифмической линейке длиной 250 мм ошибка не превышает 0 1 мм. Таким образом, обычно бывает известна максимальная абсолютная погрешность, получаемая при измерении величины х; обозначим эту погрешность через их.