Как определить вязкость жидкости методом стокса?

Содержание:

Коэффициенты вязкости среды
Вязкость газов
- Вязкость некоторых газов (при 0°C)
Определение вязкости масла
Коэффициент вязкости: формула
Динамическая вязкость
Вязкость аморфных материалов[ | ]
Вязкость аморфных материалов
От чего зависит вязкость масла
Полезные советы
Примеры задач с решением
Связь динамической и кинематической вязкости
- Измерение вязкости
- От чего зависит значение величины вязкости?
Вязкость газов
- Влияние температуры на вязкость газов
Вязкость газов
- Влияние температуры на вязкость газов
Вязкость. Пояснения. Абсолютная и кинематическая вязкость. Таблицы значений вязкости — мало, школьный вариант. Вариант для печати.

Коэффициенты вязкости среды

Взаимодействие слоев среды друг на друга сказывается на характеристиках всей системы жидкости или газа. Вязкость – это один из примеров такого физического явления, как трение. Благодаря ей верхние и нижние слои среды постепенно выравнивают скорости своего тока, и в конечном итоге она приравнивается к нулю. Также вязкость можно характеризовать как сопротивление одного слоя среды другому.

Для описания таких явлений выделяют две качественные характеристики внутреннего трения:

динамический коэффициент вязкости (динамическая вязкость жидкости);
кинетический коэффициент вязкости (кинетическая вязкость).

Обе величины связаны уравнением υ = η / ρ, где ρ – плотность среды, υ – кинетическая вязкость, а η – динамическая вязкость.

Вязкость газов

Вязкость газов (явление внутреннего трения) — это появление сил трения между слоями газа, движущимися друг относительно друга параллельно и с разными по величине скоростями. Вязкость газов увеличивается с ростом температуры

Взаимодействие двух слоев газа рассматривается как процесс, в ходе которого от одного слоя к другому передается импульс. Сила трения на единицу площади между двумя слоями газа, равная импульсу, передаваемому за секунду от слоя к слою через единицу площади, определяется законом Ньютона:

τ=-η•dν/_dz

где:
dν/_dz — градиент скорости в направлении перпендикулярном направлению движения слоев газа.
Знак минус указывает, что импульс переносится в направлении убывания скорости.
η — динамическая вязкость.

η=1/₃•ρ(ν)•λ,

ρ — плотность газа,
(ν) — средняя арифметическая скорость молекул
λ — средняя длина свободного пробега молекул.

Вязкость некоторых газов (при 0°C)

Вещество	Вязкость 10 -5 кг/(м*с)
Азот	1,67
Аммиак	0,93
Водород	0,84
Воздух	1,72
Гелий	1,89
Гелий	1,89
Кислород	1,92
Метан	1,04
Углекислый газ	1,40
Хлор	1,29

Определение вязкости масла

О том, что любой смазочный материал должен препятствовать такому явлению, как сухое трение между движущимися и соприкасающимися деталями, знают даже школьники. В отношении автомобильного двигателя задача масла соответствующая – уменьшить силу трения в цилиндропоршневой группе при обеспечении максимальной герметичности цилиндров. Решение этой задачи не выглядит тривиальным, поскольку силовой агрегат вынужден работать в очень широком температурном диапазоне, от минусовых (холодный двигатель, пуск зимой) до плюс 300ºС – такой режим характерен для некоторых узлов прогретого мотора.

Отметим, что многие водители убеждены, что та температура, которая отображается на шкале прибора, измеряет температуру самого двигателя. Это, конечно же, заблуждение – датчик измеряет только температуру тосола. А она действительно на прогретом моторе практически одинакова во всём контуре и составляет примерно 90 градусов. Узлы же силового агрегата греются по-разному. Соответственно, и температура моторного масла тоже «гуляет», причём в достаточно широких пределах, доходя до значений порядка 150ºС.

А поскольку современные двигатели представляют собой достаточно сложную конструкцию, их производители рекомендуют использовать смазочные жидкости с вполне определёнными эксплуатационными характеристиками. Именно они обеспечивают максимально возможный КПД двигателя за счёт уменьшения силы трения, способствуя снижению износа трущихся деталей при среднестатистических нагрузках на мотор.

И важнейшей из этих характеристик является вязкость ММ. Самое простое и понятное определение вязкости следующее: это способность масла сохранять свою текучесть в заданных условиях работы, оставаясь на поверхности трущихся деталей. Добиться этого не сложно, если бы не динамически изменяемый температурный режим: на непрогретом двигателе он один, при работе в штатном режиме – другой – при повышенных нагрузках – третий.

Понятно, что изобрести некий универсальный состав, который бы одинаково хорошо работал независимо от внешних условий, невозможно.

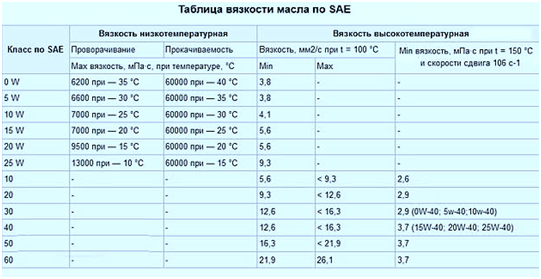
А чтобы и автопроизводители, и потребители имели возможность как-то оценивать вязкость конкретных масел, Ассоциация автоинженеров США (SAE) разработала и внедрила классификацию ММ по их вязкости, в соответствии с определёнными температурными режимами работы. Другими словами, классификация упрощает выбор масла в зависимости от предпочтительного режима эксплуатации автомобиля.

У многих водителей вызывает затруднение расшифровка вязкости масла, указываемая на маркировке смазочных жидкостей для мотора в соответствии с классификацией по SAE. Как правило она начинается с одной или двух цифр, за которыми следует буква W, а через тире следует ещё одна пара цифр.

Рассмотрим на простом и доступном уровне, что означают эти цифры в отношении вязкости масла. То, что стоит до буквы W – так называемая низкотемпературная вязкость, указывающая на возможность запуска мотора при определённой отрицательной температуре (вычислить её можно, отняв от указанной цифры значение 40). То есть 5W обозначает, что такая жидкость обеспечивает беспроблемный пуск двигателя при температуре не ниже минус 40 градусов.

Отметим, что данный показатель касается только нижнего порога температур для холодного мотора, не влияя на рабочие характеристики масла, используемого на горячем силовом агрегате. Но опять же, производители масел рассчитывают этот параметр на основании испытаний на конкретных моторах, поэтому он является, так сказать, усреднённым. В действительности всё зависит от конкретного мотора, поэтому ориентироваться нужно на рекомендации автопроизводителя, а не на маркировку. Отметим, что, если в конкретном регионе максимальные морозы не превышают -20°С, можно использовать ММ с практически любым префиксом, поскольку масла с индексом, большим 20W, встречаются на рынке очень редко.

Вторая группа цифр указывает на высокотемпературный показатель вязкости, однако здесь нет прямой зависимости от температуры. Он обозначает некий обобщённый параметр, характеризующий минимальную/максимальную вязкость ММ при функционировании в рабочем диапазоне температур (а это в среднем 100-150 градусов). Чем выше этот показатель, тем больше вязкость масла при работе в более высоком температурном режиме. А слишком жидкое масло не сможет обеспечить выполнение своих непосредственных обязанностей – смазывать трущиеся поверхности. Так что интерпретация второго пары цифр даже среди специалистов вызывает определённые разногласия, и совет придерживаться рекомендаций автопроизводителей здесь ещё более актуален.

Коэффициент вязкости: формула

В упрощенном виде процесс движения вязкой жидкости в трубопроводе можно рассмотреть в виде плоских параллельных слоев А и В с одинаковой площадью поверхности S, расстояние между которыми составляет величину h.

Эти два слоя (А и В) перемещаются с различными скоростями (V и V+ΔV). Слой А, имеющий наибольшую скорость (V+ΔV), вовлекает в движение слой B, движущийся с меньшей скоростью (V). В то же время слой B стремится замедлить скорость слоя А. Физический смысл коэффициента вязкости заключается в том, что трение молекул, представляющих собой сопротивление слоев потока, образует силу, которую Исаак Ньютон описал следующей формулой:

F = µ × S × (ΔV/h)

Здесь:

ΔV – разница скоростей движений слоев потока жидкости;
h – расстояние между слоями потока жидкости;
S – площадь поверхности слоя потока жидкости;
μ (мю) – коэффициент, зависящий от свойства жидкости, называется абсолютной динамической вязкостью.

В единицах измерения системы СИ формула выглядит следующим образом:

µ = (F × h) / (S × ΔV) = (Паскаль × секунда)

Здесь F – сила тяжести (вес) единицы объема рабочей жидкости.

Динамическая вязкость

Вязкость (внутреннее трение) возникает между двумя слоями газа или жидкости, которые перемещаются параллельно друг другу с разными скоростями в результате возникновения сил трения между ними. Вязкость обусловлена переносом молекулами из одного слоя вещества в другой количества движения.

В одномерном случае, когда $v=v\left(x\right),$ движение вещества описывают при помощи уравнения Ньютона вида:

где $dF$ — сила внутреннего трения, которая действует на площадь ($dS$) поверхностного слоя; $\frac{dv}{dx}$ — градиент скорости перемещения слоев по направлению оси X (перпендикулярно поверхностному слою); $\eta $ — коэффициент динамической вязкости.

В соответствии с классической кинетической теорией коэффициент вязкости газа равен:

где $\left\langle \lambda \right\rangle $ — средняя длина свободного пробега молекулы; $\left\langle v\right\rangle $ — средняя скорость теплового движения молекул; $\rho $ — плотность газа. В более точной теории коэффициент $\frac{1}{3}$ , заменяется на параметр ($\varphi $), который зависит от характера взаимодействия молекул в веществе. Так, если считают, что молекулы газа сталкиваются как гладкие, твердые шары, то $\varphi =0,499.$ При использовании более точных моделей коэффициент $\varphi $ является функцией от температуры вещества.

Для жидкостей выражения (2) не является справедливым. Для газов, исходя из (2) $\eta \sim \sqrt{T}$, тогда как, у жидкостей вязкость, с ростом температуры, уменьшается. Вязкость жидкости обратно пропорциональна коэффициенту диффузии (D):

где $f$ — некоторый постоянный параметр, имеющий размерность силы.

Вязкость аморфных материалов[ | ]

Вязкость аморфных материалов (например, стекла или расплавов) — это термически активизируемый процесс:

η ( T ) = A ⋅ exp ⁡ ( Q R T ) , {\displaystyle \eta (T)=A\cdot \exp \left({\frac {Q}{RT}}\right),}

где:

Q {\displaystyle Q} — энергия активации вязкости (Дж/моль);
T {\displaystyle T} — температура ();
R {\displaystyle R} — универсальная газовая постоянная (8,31 Дж/моль·К);
A {\displaystyle A} — некоторая постоянная.

Вязкое течение в аморфных материалах характеризуется отклонением от закона Аррениуса: энергия активации вязкости Q {\displaystyle Q} изменяется от большой величины Q H {\displaystyle Q_{H}} при низких температурах (в стеклообразном состоянии) на малую величину Q L {\displaystyle Q_{L}} при высоких температурах (в жидкообразном состоянии). В зависимости от этого изменения аморфные материалы классифицируются либо как сильные, когда ( Q H − Q L ) < Q L {\displaystyle \left(Q_{H}-Q_{L}\right) , или ломкие, когда ( Q H − Q L ) ≥ Q L {\displaystyle \left(Q_{H}-Q_{L}\right)\geq Q_{L}} . Ломкость аморфных материалов численно характеризуется параметром ломкости Доримуса R D = Q H Q L {\displaystyle R_{D}={\frac {Q_{H}}{Q_{L}}}} : сильные материалы имеют R D < 2 {\displaystyle R_{D}<2} , в то время как ломкие материалы имеют R D ≥ 2 {\displaystyle R_{D}\geq 2} .

Вязкость аморфных материалов весьма точно аппроксимируется двуэкспоненциальным уравнением:

η ( T ) = A 1 ⋅ T ⋅ ⋅ {\displaystyle \eta (T)=A_{1}\cdot T\cdot \left\cdot \left}

с постоянными A 1 {\displaystyle A_{1}} , A 2 {\displaystyle A_{2}} , B {\displaystyle B} , C {\displaystyle C} и D {\displaystyle D} , связанными с термодинамическими параметрами соединительных связей аморфных материалов.

В узких температурных интервалах недалеко от температуры стеклования T g {\displaystyle T_{g}} это уравнение аппроксимируется формулами типа VTF или сжатыми экспонентами Кольрауша.

Вязкость

Если температура существенно ниже температуры стеклования T < T g {\displaystyle T , двуэкспоненциальное уравнение вязкости сводится к уравнению типа Аррениуса

η ( T ) = A L T ⋅ exp ⁡ ( Q H R T ) , {\displaystyle \eta (T)=A_{L}T\cdot \exp \left({\frac {Q_{H}}{RT}}\right),}

с высокой энергией активации Q H = H d + H m {\displaystyle Q_{H}=H_{d}+H_{m}} , где H d {\displaystyle H_{d}} — энтальпия разрыва соединительных связей, то есть создания конфигуронов, а H m {\displaystyle H_{m}} — энтальпия их движения. Это связано с тем, что при T < T g {\displaystyle T аморфные материалы находятся в стеклообразном состоянии и имеют подавляющее большинство соединительных связей неразрушенными.

При T ≫ T g {\displaystyle T\gg T_{g}} двуэкспоненциальное уравнение вязкости также сводится к уравнению типа Аррениуса

η ( T ) = A H T ⋅ exp ⁡ ( Q L R T ) , {\displaystyle \eta (T)=A_{H}T\cdot \exp \left({\frac {Q_{L}}{RT}}\right),}

но с низкой энергией активации Q L = H m {\displaystyle Q_{L}=H_{m}} . Это связано с тем, что при T ≫ T g {\displaystyle T\gg T_{g}} аморфные материалы находятся в расправленном состоянии и имеют подавляющее большинство соединительных связей разрушенными, что облегчает текучесть материала.

Вязкость аморфных материалов

Вязкость аморфных материалов (например, стекла или расплавов) — это термически активизируемый процесс:

η ( T ) = A ⋅ exp ⁡ ( Q R T ) , {\displaystyle \eta (T)=A\cdot \exp \left({\frac {Q}{RT}}\right),}

где:

Q {\displaystyle Q} — энергия активации вязкости (Дж/моль);
T {\displaystyle T} — температура ();
R {\displaystyle R} — универсальная газовая постоянная (8,31 Дж/моль·К);
A {\displaystyle A} — некоторая постоянная.

Вязкость аморфных материалов весьма точно аппроксимируется двуэкспоненциальным уравнением:

η ( T ) = A 1 ⋅ T ⋅ ⋅ {\displaystyle \eta (T)=A_{1}\cdot T\cdot \left\cdot \left}

Вязкость

η ( T ) = A L T ⋅ exp ⁡ ( Q H R T ) , {\displaystyle \eta (T)=A_{L}T\cdot \exp \left({\frac {Q_{H}}{RT}}\right),}

При T ≫ T g {\displaystyle T\gg T_{g}} двуэкспоненциальное уравнение вязкости также сводится к уравнению типа Аррениуса

η ( T ) = A H T ⋅ exp ⁡ ( Q L R T ) , {\displaystyle \eta (T)=A_{H}T\cdot \exp \left({\frac {Q_{L}}{RT}}\right),}

От чего зависит вязкость масла

Степень густоты продукта напрямую зависит от внедренных технологий и присадок во время компоновки формулы. Однако ключевыми принято считать такие факторы.

Основа.Существует три разновидности базовых групп масел. Все отличаются по изначальной густоте.

Минеральная – изготавливается путем перегонки сернистых пород нефти и преимущественно используется летом. В холодное время года быстро кристаллизуется, что делает ее эксплуатацию невозможной.
Полусинтетика – более современная технология. Популярными представителями являются гидрокрекинговые масла. Степень вязкости здесь допускает применение зимой, однако защита от перепадов температуры недостаточна.
Синтетика – передовая технология, показывающая новый технологический уровень, где внедрена процедура расщепления молекул природного газа или рапсовых соков, для получения сложных углеводородов. Эти автомасла выделяются повышенной текучестью и стойкостью к суровым климатическим условиям.

Присадки.Дополнительные включения в современных смазках в 80% имеют ключевое значение. Депрессорные компоненты стабилизируют поведение смеси во время перепадов температур, однако зависимость индекса вязкости от них мала.

Густота лубриканта зависит от комплекса технологических решений и подбора компонентов формулы.

Полезные советы

Разобравшись с тем, что такое вязкость масла и как она определяется по SAE, следует также рассмотреть некоторые нюансы и особенности при подборе смазочного материала. Прежде всего, если раньше по вязкости можно было определить, какую основу имеет масло (минеральное, полусинтетическое или синтетическое), сегодня ситуация изменилась.

Если несколько лет назад 15W40 было минеральным маслом, 10W40 полусинтетикой, а 5W40 только синтетическим, в данный момент 15W40 вполне может быть полусинтетикой, а 10W40 синтетическим маслом.

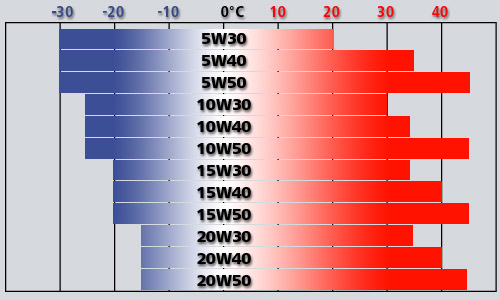
Если рассматривать сами цифры вязкости масла, вязкость по SAE предполагает, что первая цифра это зимний параметр и указывает на минимальную температуру безопасного холодного пуска ДВС. Другими словами, чем меньшей будет первая цифра, тем ниже допускается температура, когда такое масло можно использовать. Например, масла 0W будут оставаться намного более жидкими на холоде, чем 10W.

Вторая цифра, указывающая на летний параметр, четко указывает на возможность использования масла при определенных температурных условиях

Обратите внимание, как зимняя, так и летняя вязкость в маркировке не указывает на конкретные температуры окружающей среды!. Если просто, например, масло 5W30 никак не означает, что его можно использовать только при температурах окружающей среды от -5 до +30

Данные цифры к температуре окружающей среды не имеют отношения и являются условными. Чтобы точно понять, в каком температурном диапазоне способна работать та или иная смазка, нужно отдельно изучать таблицу масел по SAE

Если просто, например, масло 5W30 никак не означает, что его можно использовать только при температурах окружающей среды от -5 до +30. Данные цифры к температуре окружающей среды не имеют отношения и являются условными. Чтобы точно понять, в каком температурном диапазоне способна работать та или иная смазка, нужно отдельно изучать таблицу масел по SAE.

Если остановиться на подборе масла по вязкости, важно отдельно изучить информацию в мануале к автомобилю. Необходимо понимать, что в конкретном двигателе можно использовать только масла определенной вязкости

Как правило, производитель допускает сразу несколько вариантов с поправкой на разные условия эксплуатации. Например, в мануале может быть указано, что в двигатель рекомендуется заливать как 5W30, так и 10W40 и т.д.

При этом мнение о том, что чем больше пробег, тем гуще масло в двигатель нужно заливать, часто является не совсем верным. Если производитель по мануалу допускает увеличение вязкости и указывает доступные варианты, тогда вполне можно к 100-150 тыс. пробега перейти, например, с 5W30 на 5W40 или на 10W40 после 200 тыс. км.

Однако если в мануале указано, что в двигатель можно лить только 5W30, тогда даже к 200 тыс. км. пробега и более нужно заливать только такое масло. Дело в том, что многие двигатели могут иметь тонкие и удлиненные масляные каналы.

Если залить масло гуще, чем рекомендуется производителем авто, маслонасос может не прокачать более вязкое масло в нужном объеме (особенно после холодного пуска), мотор начнет работать в условиях масляного голодания и т.д. Само собой, будет ускорен износ деталей и произойдет заметное сокращение моторесурса.

Единственным случаем, когда можно намеренно использовать не рекомендованное густое масло, принято считать сильный износ мотора, который и так уже идет на «капиталку». Такое решение иногда позволяет немного отсрочить сам ремонт и сократить расход масла на долив.

Однако переход на более вязкие масла можно осуществить только после консультации с опытным мотористом, так как всегда есть риск еще сильнее повредить ДВС, что также повысит последующие затраты на ремонт. Если же двигатель исправен, тогда следует лить только такое масло по вязкости, которое рекомендовано самим производителем автомобиля.

Примеры задач с решением

Пример 1

Задание. Получите единицу измерения динамической вязкости жидкости, используя выражение связывающее коэффициент вязкости и коэффициент диффузии.

Решение. В качестве основы для решения задачи (по ее условию) мы будем использовать формулу, которая определяет коэффициент динамической вязкости жидкости:

где $\left=Н$; $\left=\frac{м^2}{с}$. В основных единицах системы СИ, ньютон выражается как:

Используя выражение (1.1), получаем:

\=\frac{\left}{\left}=\frac{кг\cdot м}{с^2}\cdot \frac{с}{м^2}=\frac{кг}{с\cdot м}=\frac{кг}{с^2\cdot м}\cdot с=Па\cdot с.\]

Ответ. Мы получили, что $Па\cdot с$ — единица измерения динамической вязкости жидкости.

Пример 2

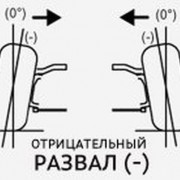
Задание. Маленький шарик, плотность которого $\rho $, радиус $r$ всплывает в сосуде, наполненном жидкостью (${\rho }_j$ — плотность жидкости). Скорость движения шарика постоянна и равна $v$. Какова динамическая вязкость жидкости ($\eta $)? Используя полученную формулу, проверьте, в каких единицах измеряется полученная вязкость.

Решение. Изобразим силы, действующие на шарик при его движении в жидкости. Это сила тяжести ($m\overline{g}$); сила Архимеда (${\overline{F}}_A$); сила Стокса (сила вязкого трения) ($\overline{F}$).

По второму закону Ньютона (учитывая, что шарик движется равномерно) имеем:

Запишем проекцию уравнения (1.1) на ось Y:

где:

Следовательно:

Используя полученное выражение для коэффициента вязкости ($\eta =\frac{{2r}^2g}{9v}\left({\rho }_j-\rho \right)$) определим единицу измерения для $\eta $:

\=\left=\frac{\left\left}{\left}\left(\left\right)=\frac{м^2\cdot \frac{м}{с^2}}{{м}/{с}}\cdot \frac{кг}{м^3}=\frac{кг}{м\cdot с}=Па\cdot с.\]

Ответ. $\eta =\frac{{2r}^2g}{9v}\left({\rho }_j-\rho \right)$

Связь динамической и кинематической вязкости

Вязкость жидкости определяет способность жидкости сопротивляться сдвигу при ее движении, а точнее сдвигу слоев относительно друг друга

Поэтому на производствах, где требуется перекачка различных сред, важно точно знать вязкость перекачиваемого продукта и правильно подбирать насосное оборудование

В технике встречаются два вида вязкости.

Кинематическая вязкость чаще используется в паспорте с характеристиками жидкости.
Динамическая используется в инженерных расчетах оборудования, научно-исследовательских работах и т.д.

Перевод кинематической вязкости в динамическую производят с помощью формулы, указанной ниже, через плотность при заданной температуре:

Где:

v – кинематическая вязкость,

n – динамическая вязкость,

p – плотность.

Таким образом, зная ту или иную вязкость и плотность жидкости можно выполнить пересчет одного вида вязкости в другой по указанной формуле или через конвертер выше.

Измерение вязкости

Понятия для этих двух типов вязкости присуще только жидкостям в связи с особенностями способов измерения.

Измерение кинематической вязкости используют метод истечения жидкости через капилляр (например используя прибор Уббелоде). Измерение динамической вязкости происходит через измерение сопротивление движения тела в жидкости (например сопротивление вращению погруженного в жидкость цилиндра).

От чего зависит значение величины вязкости?

Вязкость жидкости зависит в значительной мере от температуры. С увеличением температуры вещество становится более текучим, то есть менее вязким. Причем изменение вязкости, как правило, происходит достаточно резко, то есть нелинейно.

Поскольку расстояние между молекулами жидкого вещества намного меньше, чем у газов, у жидкостей уменьшается внутреннее взаимодействие молекул из-за снижения межмолекулярных связей.

Форма молекул и их размер, а также взаимоположение и взаимодействие могут определять вязкость жидкости. Также влияет их химическая структура.

Например, для органических соединений вязкость возрастает при наличии полярных циклов и групп.

Для насыщенных углеводородов – рост происходит при “утяжелении” молекулы вещества.

Вязкость газов

В кинетической теории газов коэффициент внутреннего трения вычисляется по формуле

η = 1 3 ⟨ u ⟩ ⟨ λ ⟩ ρ {\displaystyle \eta ={\frac {1}{3}}\langle u\rangle \langle \lambda \rangle \rho } ,

где ⟨ u ⟩ {\displaystyle \langle u\rangle } — средняя скорость теплового движения молекул, ⟨ λ ⟩ {\displaystyle \langle \lambda \rangle } − средняя длина свободного пробега. Из этого выражения в частности следует, что вязкость не очень разреженных газов практически не зависит от давления, поскольку плотность ρ {\displaystyle \rho } прямо пропорциональна давлению, а ⟨ λ ⟩ {\displaystyle \langle \lambda \rangle } — обратно пропорциональна. Такой же вывод следует и для других кинетических коэффициентов для газов, например, для коэффициента теплопроводности. Однако этот вывод справедлив только до тех пор, пока разрежение газа не становится столь малым, что отношение длины свободного пробега к линейным размерам сосуда (число Кнудсена) не становится по порядку величины равным единице; в частности, это имеет место в сосудах Дьюара (термосах).

С повышением температуры вязкость большинства газов увеличивается, это объясняется увеличением средней скорости молекул газа u {\displaystyle u} , растущей с температурой как T {\displaystyle {\sqrt {T}}}

Влияние температуры на вязкость газов

В отличие от жидкостей, вязкость газов увеличивается с увеличением температуры (у жидкостей она уменьшается при увеличении температуры).

Формула Сазерленда

может быть использована для определения вязкости идеального газа в зависимости от температуры:

μ = μ 0 T 0 + C T + C ( T T 0 ) 3 / 2 , {\displaystyle {\mu }={\mu }_{0}{\frac {T_{0}+C}{T+C}}\left({\frac {T}{T_{0}}}\right)^{3/2},}

где:

μ — динамическая вязкость в (Па·с) при заданной температуре T;
μ0 — контрольная вязкость в (Па·с) при некоторой контрольной температуре T0;
T — заданная температура в Кельвинах;
T0 — контрольная температура в Кельвинах;
C — постоянная Сазерленда для того газа, вязкость которого требуется определить.

Эту формулу можно применять для температур в диапазоне 0 < T < 555 K и при давлениях менее 3,45 МПа с ошибкой менее 10 %, обусловленной зависимостью вязкости от давления.

Постоянная Сазерленда и контрольные вязкости газов при различных температурах приведены в таблице ниже:

Газ	C, K	T0, K	μ0, мкПа·с
Воздух	120	291,15	18,27
Азот	111	300,55	17,81
Кислород	127	292,25	20,18
Углекислый газ	240	293,15	14,8
Угарный газ	118	288,15	17,2
Водород	72	293,85	8,76
Аммиак	370	293,15	9,82
Оксид серы(IV)	416	293,65	12,54
Гелий	79,4	273	19

Вязкость газов

В кинетической теории газов коэффициент внутреннего трения вычисляется по формуле

η=13⟨u⟩⟨λ⟩ρ{\displaystyle \eta ={\frac {1}{3}}\langle u\rangle \langle \lambda \rangle \rho },

где ⟨u⟩{\displaystyle \langle u\rangle } — средняя скорость теплового движения молекул, ⟨λ⟩{\displaystyle \langle \lambda \rangle } − средняя длина свободного пробега. Из этого выражения в частности следует, что вязкость не очень разреженных газов практически не зависит от давления, поскольку плотность ρ{\displaystyle \rho } прямо пропорциональна давлению, а ⟨λ⟩{\displaystyle \langle \lambda \rangle } — обратно пропорциональна. Такой же вывод следует и для других кинетических коэффициентов для газов, например, для коэффициента теплопроводности. Однако этот вывод справедлив только до тех пор, пока разрежение газа не становится столь малым, что отношение длины свободного пробега к линейным размерам сосуда (число Кнудсена) не становится по порядку величины равным единице; в частности, это имеет место в сосудах Дьюара (термосах).

С повышением температуры вязкость большинства газов увеличивается, это объясняется увеличением средней скорости молекул газа u{\displaystyle u}, растущей с температурой как T{\displaystyle {\sqrt {T}}}

Влияние температуры на вязкость газов

Формула Сазерленда может быть использована для определения вязкости идеального газа в зависимости от температуры:

μ=μT+CT+C(TT)32,{\displaystyle {\mu }={\mu }_{0}{\frac {T_{0}+C}{T+C}}\left({\frac {T}{T_{0}}}\right)^{3/2},}

где:

μ — динамическая вязкость в (Па·с) при заданной температуре T;
μ — контрольная вязкость в (Па·с) при некоторой контрольной температуре T;
T — заданная температура в Кельвинах;
T — контрольная температура в Кельвинах;
C — постоянная Сазерленда для того газа, вязкость которого требуется определить.

Постоянная Сазерленда и контрольные вязкости газов при различных температурах приведены в таблице ниже:

Газ	C, K	T, K	μ, мкПа·с
Воздух	120	291,15	18,27
Азот	111	300,55	17,81
Кислород	127	292,25	20,18
Углекислый газ	240	293,15	14,8
Угарный газ	118	288,15	17,2
Водород	72	293,85	8,76
Аммиак	370	293,15	9,82
Оксид серы(IV)	416	293,65	12,54
Гелий	79,4	273	19

Вязкость. Пояснения. Абсолютная и кинематическая вязкость. Таблицы значений вязкости — мало, школьный вариант. Вариант для печати.

Кинематическая вязкость — мера потока имеющей сопротивление жидкости под влиянием силы тяжести. Когда две жидкости равного объема помещены в идентичные капиллярные вискозиметры и двигаются самотеком, вязкой жидкости требуется больше времени для протекания через капилляр. Если одной жидкости требуется для вытекания 200 секунд,а другой — 400 секунд, вторая жидкость в два раза более вязкая, чем первая по шкале кинематической вязкости.
- Размерность кинематической вязкости — L2/T, где L — длина, и T — время. Обычно используется сантистокс (cSt). ЕДИНИЦА СИ кинематической вязкости — mm2/s, = 1 cSt =1 сантиСтокс = 10-6м2/с = мм2/с
- Перевод единиц кинематической вязкости

Абсолютная (динамическая) вязкость, иногда называемая динамической или простой вязкостью, является произведением кинематической вязкости и плотности жидкости:
- Абсолютная вязкость = Кинематическая вязкость * Плотность
- Абсолютная вязкость выражается в сантипуазах (сПуаз). ЕДИНИЦА СИ абсолютной вязкости — Паскаль-секунда (Pa-s), запомним, что 1 сПуаз = 1 mPa-s.
- Перевод единиц динамической = абсолютной вязкости

Вязкость газов при атмосферном давлении:
η, 10 -6 Па· с	150 К	200 К	250 К	300 К	400 К
Азот	10.0	12.9	15.5	17.9	22.1
Аммиак	—	6.89	8.53	10.3	13.9
Аргон	12.3	16.0	19.5	22.7	28.5
Ацетилен	—	—	—	10.3	13.5
Бромметан	—	—	13.2	15.8	20.2
Водород	5.57	6.78	7.90	8.94	10.9
Водяной пар	—	—	—	9.13	13.2
Воздух	10.3	13.2	16.0	18.5	23.0
Гелий	12.3	15.0	17.5	19.9	24.3
Кислород	11.3	14.6	17.8	20.7	25.9
Метан	—	7.76	9.53	11.2	14.2
Неон	19.4	23.9	28.0	31.7	38.4
Оксид азота (II)	10.5	13.6	16.6	19.3	24.1
Оксид углерода (II)	9.84	12.7	15.4	17.8	22.1
Оксид углерода (IV)	—	10.2	12.6	15.0	19.5
Пропан	—	—	7.1	8.3	9.5
Этан	—	6.43	7.96	9.45	12.2
Этилен	—	7.1	8.8	10.4	13.5

Вязкость жидкостей при атмосферном давлении:
η, 10 -3 Па· с	0°C	20°C	50°C	70°C	100°C
Ацетон	=	0.32	0.25	=	=
Бензин	0.73	0.52	0.37	0.26	0.22
Бензол	=	0.65	0.44	0.35	=
Вода	1.80	1.01	0.55	0.41	0.28
Глицерин	12100	1480	180	59	13
Керосин	2.2	1.5	0.95	0.75	0.54
Кислота уксусная	=	1.2	0.62	0.50	0.38
Масло касторовое	=	987	129	49	=
Пентан	0.28	0.24	=	=	=
Ртуть	=	1.54	1.40	=	1.24
Спирт метиловый	0.82	0.58	0.4	0.3	0.2
Спирт этиловый (96%)	1.8	1.2	0.7	0.5	0.3
Толуол	=	0.61	0.45	0.37	0.29

Вязкость расплавов:
	t°, °C	η, 10 -3 Па· с
Алюминий	700	2.90
Висмут	305	1.65
Калий	100	0.46
Натрий	105	0.69
Олово	240	1.91
Свинец	440	2.11
Цинк	430	3.3
Бромид ртути	250	3.0
Бромид свинца	380	10.2
Бромид серебра	610	1.86
Гидроксид калия	400	2.3
Гидроксид натрия	350	4.0
Хлорид калия	790	1.4
Хлорид натрия	320	2.83
Хлорид серебра	600	1.61

Вязкость воды:
t°, °C	η, 10 -6 Па· с
1797
10	1307
20	1004
30	803
40	655
50	551
60	470
70	407
80	357
90	317
100	284
110	256
120	232
130	212
140	196
150	184

Динамическая вязкость воздуха:
η, 10 -6 Па· с	температура воздуха
давление	0°C	25°C	100°C
1 атм	17.20	18.37	21.80
20 атм	17.53	18.65	22.02
50 атм	18.15	19.22	22.40
100 атм	19.70	20.60	23.35
200 атм	23.70	23.95	25.30