Сила сопротивления

Что такое сила сопротивления в физике

Сила сопротивления — сила, которая возникает во время движения тела в жидкой или газообразной среде и препятствует этому движению.

Важно уметь отличать силу сопротивления от силы трения. Во втором случае рассматривается характер взаимодействия твердых тел друг с другом

Таким образом, трение можно наблюдать, когда какой-либо предмет перемещается по поверхности другого. Вектор этой силы будет направлен в противоположную сторону направления движения.

Для того чтобы рассчитать силу сопротивления необходимо умножить коэффициент сопротивления материала на силу, провоцирующую перемещение этого предмета.

Примечание

В качестве примера силы сопротивления можно рассмотреть движение поезда. Воздух, окружающий состав, замедляет скорость его перемещения, то есть возникает сила сопротивления.

От чего зависит в механике и динамике

Сила сопротивления зависит от нескольких факторов. На ее величину оказывают влияния следующие характеристики:

1. Особенности среды и показатели ее плотности, к примеру, жидкость обладает большей плотностью, чем газообразное вещество.
2. Форма тела, так как предметы, обладающие обтекаемыми вытянутыми вдоль направления движения формами подвержены меньшему сопротивлению, чем тела с множеством плоскостей, расположенных перпендикулярно движению.
3. Скорость перемещения тела.

Силу сопротивления можно наблюдать опытным путем. К примеру, если предмет переместился на величину пути l , когда на него воздействует сила сопротивления, обозначение которой представлено, как \($$F_{r}$$\), затрачивается работа, которую можно рассчитать по формуле:

\($$A=F_{r}\times l$$\)

В случае, когда площадь поперечного сечения движущегося предмета равна S, он будет сталкиваться с частицами, объем которых составляет Sl. Полную массу этих частиц можно представить, как \($$\rho_{ a}\times Sl$$\). Если частицы полностью увлекаются телом, они приобретают скорость V. Кинетическую энергию можно рассчитать по формуле:

\($$K=\frac{\rho_{ a}\times Sl\times V^{2}}{2}$$\)

Энергию создают внешние силы за счет своей работы с мощностью по определению силы сопротивления. Откуда, A=K. Таким образом,

\($$F_{r}=\frac{\rho_{ a}\times S\times V^{2}}{2}$$\)

В этом случае зависимость силы сопротивления от скорости перемещения объекта возрастает и становится пропорциональна ее второй степени. В отличие от силы внутреннего трения ее обозначают, как силу динамического лобового сопротивления.

Следует отметить, что теория, в которой частицы среды полностью увлекаются транспортируемыми телами, преувеличена. В условиях реального времени любой движущийся предмет обтекаем потоком, который снижает воздействие на него сил сопротивления. Поэтому при расчетах нередко используют коэффициент сопротивления С, обозначая силу лобового сопротивления формулой:

\($$F_{r}=C\times S\times \frac{\rho_{ a}\times V^{2}}{2}$$\)

ФИЗИКА

§ 3.15. Сила сопротивления при движении тел в жидкостях и газах

При движении твердого тела в жидкости или газе или при движении одного слоя жидкости (газа) относительно другого тоже возникает сила, тормозящая движение, — сила жидкого трения или сила сопротивления.

Сила сопротивления направлена параллельно поверхности соприкосновения твердого тела с жидкостью (газом) в сторону, противоположную скорости тела относительно среды, и тормозит движение(1).

Сила сопротивления (жидкого трения) обычно значительно меньше силы сухого трения. Именно поэтому для уменьшения сил трения между движущимися деталями машин применяют смазку.

Главная особенность силы сопротивления состоит в том, что она появляется только при относительном движении тела и окружающей среды. Сила трения покоя в жидкостях и газах полностью отсутствует. Это приводит к тому, что усилием рук можно сдвинуть тяжелое тело, например баржу, в то время как сдвинуть с места, скажем, гусеничный трактор усилием рук просто невозможно.

Убедитесь в том, что плавающий деревянный брусок сразу же придет в движение, если на него слегка подуть. Попробуйте проделать то же самое с бруском, лежащим на столе.

Модуль силы сопротивления _c зависит от размеров, формы и состояния поверхности тела, свойств (вязкости) среды (жидкости или газа), в которой движется тело, и, наконец, от относительной скорости движения тела и среды.

Для того чтобы уменьшить силу сопротивления среды, телу придают обтекаемую форму. Наиболее выгодна в этом отношении сигарообразная форма (рис. 3.40), близкая к форме падающей капли дождя или рыбы.

Рис. 3.40

Влияние формы тела на силу сопротивления наглядно показано на рисунке 3.41. Модуль силы сопротивления цилиндра обозначим через . Конусообразная насадка к цилиндру уменьшает силу сопротивления от 1/2 до 1/4 в зависимости от размера угла при вершине конуса. Сглаженная насадка доводит силу сопротивления до 1/5. Наконец, если придать телу сигарообразную форму, то при том же поперечном сечении сила сопротивления уменьшается до 1/25. По сравнению с телом сигарообразной формы сила сопротивления для шара (имеющего такую же площадь поперечного сечения) больше в несколько раз, а для тонкого диска, плоскость которого перпендикулярна направлению скорости, — в несколько десятков раз. Особенно велика сила сопротивления, возникающая при движении полусферы вогнутой стороной вперед. По этой причине парашюты имеют часто форму полусферы.

Рис. 3.41

Примерный характер зависимости модуля силы сопротивления от модуля относительной скорости тела приведен на рисунке 3.42. Если тело неподвижно относительно вязкой среды (относительная скорость равна нулю), то сила сопротивления равна нулю. С увеличением относительной скорости сила сопротивления растет медленно, а потом все быстрее и быстрее.

Рис. 3.42

При малых скоростях движения в жидкости (газе) силу сопротивления можно считать приближенно прямо пропорциональной скорости движения тела относительно среды:

где k₁ — коэффициент сопротивления, зависящий от формы, размеров, состояния поверхности тела и свойств среды — ее вязкости. Коэффициент k₂ в СИ выражается в Н • с/м = кг/с. Его значение определяют опытным путем.

При больших скоростях относительного движения сила сопротивления пропорциональна квадрату скорости:

где коэффициент сопротивления k₂ выражается в Н • с2/м2 = = кг/м.

Какую именно формулу следует применять в данном конкретном случае, устанавливают опытным путем. При падении тел в воздухе сила сопротивления становится пропорциональной квадрату скорости практически с самого начала падения.

При ускоренном движении тела в жидкости для учета воздействия жидкости на это тело надо к массе тела прибавить так называемую присоединенную массу. Присоединенная масса зависит от формы тела и плотности среды. В дальнейшем при решении задач присоединенную массу мы учитывать не будем.

Жидкое трение возникает между поверхностью твердого тела и окружающей его жидкой или газообразной средой, в которой оно движется. При медленном движении сила сопротивления пропорциональна скорости, а при быстром — квадрату скорости.

(1) Впрочем, движущийся поток воды или воздуха может увлекать за собой тело. Например, когда ветер гонит опавшие листья, то сила трения со стороны воздуха направлена по движению листьев. Но и в этом случае она противоположна скорости движения тела (листьев) относительно среды (воздуха). В приведенном примере воздух и листья, хотя и движутся в одном направлении, но скорость воздуха больше, листья отстают от ветра.

Свободное падение

Свободное падение — частный случай равноускоренного прямолинейного движения. Если тело отпустить с некоторой высоты, оно будет падать с ускорением свободного падения без начальной скорости. Тогда его кинематические величины можно определить по следующим формулам:

Скорость

v = gt

v — скорость, g — ускорение свободного падения, t — время, в течение которого падало тело

Пример №1. Тело упало без начальной скорости с некоторой высоты. Найти его скорость в конечный момент времени t, равный 3 с.

Подставляем данные в формулу и вычисляем:

v = gt = 10∙3 = 30 (м/с).

Перемещение при свободном падении тела равно высоте, с которой оно начало падать. Высота обозначается буквой h.

Внимание! Перемещение равно высоте, с которой падало тело, только в том случае, если t — полное время падения. Высота падения

Высота падения

Если известна скорость падения тела в момент времени t, перемещение (высота) определяется по следующей формуле.

Если скорость тела в момент времени t неизвестна, но для нахождения перемещения (высоты) используется формула:

Если неизвестно время, в течение которого падало тело, но известна его конечная скорость, перемещение (высота) вычисляется по формуле:

Пример №2. Тело упало с высоты 5 м. Найти его скорость в конечный момент времени.

Так как нам известна только высота, и найти нужно скорость, используем для вычислений последнюю формулу. Выразим из нее скорость:

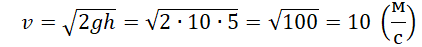
Формула определения перемещения тела в n-ную секунду свободного падения:

s(n) — перемещение за секунду n.

Пример №3. Определить перемещение свободно падающего тела за 3-ую секунду движения.

Формула закона Ома

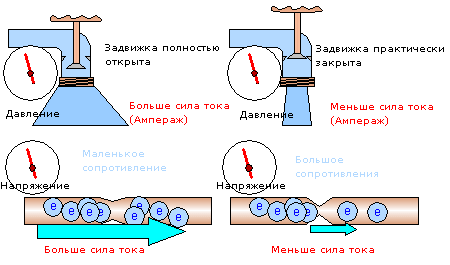
Свои опыты Ом направлял на изучение такой физической величины, как сопротивление, в результате чего в 1826 году он стал автором закона, который не потерял совей актуальность вплоть до сегодняшнего дня. Из своих опытов Ом вывел, что в различных цепях сила тока может возрастать с различной скоростью, и происходит это по мере увеличения напряжения.

Также, Ом сделал вывод, что каждый проводник обладает индивидуальными свойствами проводимости.

Сопротивление обозначается заглавной латинской и измеряется в Омах. Сопротивление – физическая величина, характеризующая свойства проводника оказывать влияние на идущий по нему ток. Оно прямо пропорционально напряжению  в сети и обратно пропорционально  силе тока. В виде формулы данный закон можно записать как R = U/I, где U – напряжение, а I – сила тока. 1 Ом равняется 1 Вольту, деленному на 1 Ампер.

Запомните! Реостат – прибор, обеспечивающий возможность изменять сопротивление. Прежде всего, он влияет на показатель R в цепи, а, следовательно, на 2 другие величины, описанные в законе Ома. Силу тока может помочь определить амперметр.

Ползунковый реостат

Из формулы закона Ома можно вывести практически любую зависимость, связанную с электричеством. Также, существует понятие удельного сопротивления проводника – физической величины, которая демонстрирует, каким сопротивлением будет обладать проводник из определенного вещества. Обозначается эта величина буквой ρ и через неё можно также найти сопротивление в цепи как произведению удельного сопротивления и длины проводника, деленного на площадь его поперечного сечения.

Важно! В виде формулы нахождение сопротивления через удельное сопротивление выглядит так: R = ρ*(l/S), где l – длина проводника, а S – площадь поперечного сечения. Физический смысл удельного сопротивления показывает, какое влияние будет оказывать проводник длиной в 1 м с площадью поперечного сечения в 1 квадратный мм, изготовленный из определенного вещества

Измеряется в Омах, умноженных на метр: =

Физический смысл удельного сопротивления показывает, какое влияние будет оказывать проводник длиной в 1 м с площадью поперечного сечения в 1 квадратный мм, изготовленный из определенного вещества. Измеряется в Омах, умноженных на метр: = .

Ом и формула

Расчет сил тяги исопротивления движениюСтраница 1

При расчете тяговой силы (РТ) пользуются значениями скоростной характеристики двигателя.

Для расчета эффективной тяговой силы необходимо знать значения радиуса колеса (rк), передаточного числа трансмиссии и скорость движения автомобиля на различных передачах при различных частотах вращения коленчатого вала двигателя.

Радиус колеса для различных типов шин может быть определен по ГОСТ, в котором регламентированы статические радиусы для ряда значений нагрузки и давления воздуха в шинах.

Кроме того, радиус колеса (в метрах), можно рассчитать по номинальным размерам шины, используя выражение:

rк = 0,5d+∆·λш·Вш = 0,5·0,4064+0,75·0,87·0,225=0,35, (2.1)

где d – диаметр обода колеса, м;

Вш – ширина профиля шины, м;

∆=Н/В — отношение высоты профиля к ширине в процентах;

λш – коэффициент смятия шины (для стандартных шин легковых автомобилей λш = 0,84…0,88)

Для определения скорости движения задается ряд значений частоты вращения коленчатого вала двигателя (ne, об/мин): 500, 1000, 1500, .,nемах. Значения скорости движения (Vа, м/с), соответствующие указанному ряду частот, рассчитывают по формуле:

, (2.2)

где Va – скорость автомобиля, м/с;

iтр — передаточное отношение трансмиссии.

м/с,

Передаточное отношение трансмиссии автомобиля определяется передаточным отношением основной коробки передач (iк), делителя (iд) и главной передачи (iо):

iтр = iк× iд× iо , (2.3)

где iк – передаточное число основной коробки передач;

iд – передаточное число дополнительной коробки передач (раздаточная коробка, делитель, демультипликатор);

iг – передаточное число главной передачи.

iI = 3,636·3,9 = 14,18,

iII = 1,95·3,9 = 7,605,

iIII = 1,357·3,9 = 5,29,

iIV = 0,941·3,9 = 3,67,

iV = 0,784·3,9 = 3,06,

Движение автотранспортного средства определяется действием сил тяги и сопротивления движению. Совокупность всех сил, действующих на автомобиль, выражает уравнения силового баланса:

Рi = Рд+ Ро+ Pтр+ Р+ Pw + Pj ,(2.4)

где: Pi — индикаторная сила тяги, H;

Рд, Ро, Pтр, P, Pw, Pj — соответственно силы сопротивления двигателя, вспомогательного оборудования, трансмиссии, дороги, воздуха и инерции, H.

Значение индикаторной силы тяги можно представить в виде суммы двух сил:

Рi = Рд + Ре , (2.5)

где Pе — эффективная сила тяги, H.

Значение Pе рассчитывается по формуле:

=, (2.6)

где: Mе — эффективный крутящий момент двигателя, Нм;

r — радиус колес, м

i- передаточное число трансмиссии.

Если в задании на курсовую работу положение дроссельной заслонки не указывается, то зависимость эффективной силы тяги строят для случая работы двигателя при полной подаче топлива (100% открытии дросселя).

В этом случае, значение Mе принимают по внешней скоростной характеристике двигателя, которую можно найти в соответствующей технической литературе.

Значения силы сопротивления двигателя Рд, приведенной к ведущим колесам автомобиля, определяются по формуле:

, (2.7)

где : Vh — рабочий объём цилиндров двигателя (литраж), л;

Sп — ход поршня, м;

— число ходов поршня за один цикл (тактность ДВС);

pдо — среднее давление механических потерь при вращении вала с предельно низкой частотой (nе≈ 0), МПа;

kД — коэффициент, учитывающий увеличение давления механических потерь при повышении скорости движения поршней в цилиндрах, МПа с/м.

Силу сопротивления вспомогательного оборудования автомобиля (Pо), приведенную к ведущим колесам, определяют по формуле:

Страницы: 1 

Определение параметров конца расширения
Давление конца расширения Давление конца расширения в двигателе с воспламенением от сжатия определяется из следующего выражения: (29) где — степень последующего расширения; — средний показатель политропы расширения. (30) (31) Температура конца расширения В конце расширения температура высчитывается …

Материалы и общие условия
Для зубчатых колес трансмиссии автомобилей применяем легированные конструкционную сталь 35Х. Термической обработкой достигается высокая твердость рабочих поверхностей зубьев и необходимая прочность их вязкой сердцевины. Хромистая сталь с содержанием углерода 0,35% и более (35Х) подвергается цианиро …

Оценка рентабельности
Чистая прибыль АТП Пч, руб, Пч=Пб — Плб=Пост — 0,375*ПР = 269623,7 – 0,375*38237,5 = 255284,6 руб. где Плб — платежи в бюджет, руб. Рентабельность продаж Rп, % Rп=Пб/В*100 =1439255,4/ 8224317*100% = 17 % Рентабельность основной деятельности Rод, % Rод=Пб/(SCi+Нпд)*100 = 1439255,4/(6579453,6 + 20560 …

Уравнение координаты и скорости при свободном падении

Уравнение координаты при свободном падении позволяет вычислять кинематические параметры движения даже в случае, если оно меняет свое направление. Так как при вертикальном движении тело меняет свое положение лишь относительно оси ОУ, уравнение координаты при свободном падении принимает вид:

Уравнение скорости при свободном падении:

v_y = v_0y + g_yt

Полезные факты

• В момент падения тела на землю y = 0.
• В момент броска тела от земли y = 0.
• Когда тело падает без начальной скорости (свободно) v = 0.
• Когда тело достигает наибольшей высоты v = 0.

Построение чертежа

Решать задачи на нахождение кинематических параметров движения тела, брошенного вертикально вверх, проще, если выполнить чертеж. Строится он в 3 шага.

План построения чертежа

• Чертится ось ОУ. Начало координат должно совпадать с уровнем земли или с самой нижней точки траектории.
• Отмечаются начальная и конечная координаты тела (y и y).
• Указываются направления векторов. Нужно указать направление ускорения свободного падения, начальной и конечной скоростей.

Уравнение скорости:

–v = v – gt_пад

Уравнение координаты:

–v = v – gt

Уравнение координаты:

Тело подбросили от земли, на одной и той же высоте оно побывало дважды

Чертеж:

Интервал времени между моментами прохождения высоты h:

∆t = t₂ – t₁

Уравнение координаты для первого прохождения h:

Уравнение координаты для второго прохождения h:

Важно! Для определения знаков проекций скорости и ускорения нужно сравнивать направления их векторов с направлением оси ОУ. Пример №5

Тело падает из состояния покоя с высоты 50 м. На какой высоте окажется тело через 3 с падения?

Пример №5. Тело падает из состояния покоя с высоты 50 м. На какой высоте окажется тело через 3 с падения?

Из условия задачи начальная скорость равна 0, а начальная координата — 50.

Поэтому:

Через 3 с после падения тело окажется на высоте 5 м.

Падение тел в воздухе.

Пока
скорость падающего тела еще мала, невелика и сила сопротивления воздуха; но по
мере того, как возрастает скорость падения, эта сила быстро растет. При
некоторой скорости сила  становится равной по модулю силе , и дальше тело
падает равномерно. Скорость такого падения называют предельной скоростью
падения. Предельная скорость тем больше, чем сильнее разрежен воздух.
Поэтому тело, падающее с очень большой высоты, может в разреженных слоях
атмосферы приобрести скорость, большую предельной скорости для нижних
(плотных) слоев. Войдя в нижние слои атмосферы, тело снизит свою скорость до
значения предельной скорости для нижних слоев.

Упражнение: 68.1.
Деформировано ли тело, падающее с предельной скоростью?

Предельная скорость
падения зависит, помимо плотности атмосферы, от формы и размеров тела и от
силы притяжения тела Землей. Тела малого размера, например мелкие капли воды
(туман), пылинки, снежинки, быстро достигают своей предельной скорости (порядка
миллиметра в секунду и меньше) и затем с этой малой скоростью опускаются вниз.
Свинцовый шарик массы 10 г достигает при падении с достаточной высоты
предельной скорости 40 м/с. Капли дождя падают со скоростью, обычно не
превышающей 7—8 м/с; чем меньше капля, тем меньше и скорость ее падения; если
бы капли дождя падали в безвоздушном пространстве, то при падении на землю с
высоты 2 км они достигали бы, независимо от их размеров, скорости 200 м/с;
такой же скорости при падении с той же высоты в безвоздушном пространстве
достигло бы и всякое другое тело. При такой скорости удары капель дождя были
бы весьма неприятны!

Различие
в предельной скорости разных тел одинаковой формы, но разных размеров
объясняется зависимостью сопротивления среды от размеров тела. Оказывается,
что сопротивление приблизительно пропорционально площади поперечного сечения
тела. При одной и той же форме тела из данного материала площадь его
поперечного сечения, а значит и сила сопротивления воздуха, растет с
увеличением размеров медленнее, чем сила тяжести: площадь поперечного сечения
растет как квадрат размера, а сила тяжести — как куб размера тела. Например,
чем больше авиационная бомба, тем больше ее предельная скорость и с тем большей
скоростью она достигает земли.

Рис. 93. Сопротивление воздуха при
движении тела каплевидной формы в 30 раз меньше сопротивления при движении
круглой пластинки и в 5 раз меньше сопротивления при движении шарика того же
поперечного сечения

Наконец,
сопротивление воздуха сильно зависит и от формы тел (рис. 93, см. также §
190). Фюзеляжу самолета придают специальную обтекаемую форму, при которой
сопротивление воздуха мало. Наоборот, парашютист должен достигать земли с
небольшой скоростью. Поэтому парашюту придают такую форму, при которой сопротивление
воздуха его движению было бы возможно больше. Предельная скорость падения
человека с раскрытым парашютом составляет 5—7 м/с. Достижение предельной
скорости парашютистом происходит иначе, чем при простом падении тела. Вначале
парашютист падает с закрытым парашютом и ввиду малого сопротивления воздуха
достигает скорости в десятки метров в секунду. При раскрытии парашюта сопротивление
воздуха резко возрастает и, превосходя во много раз силу тяжести, замедляет
падение до предельной скорости.

Сопротивление
воздуха изменяет и характер движения тел, брошенных вверх. При движении тела
вверх и сила земного притяжения, и сила сопротивления воздуха направлены вниз.
Поэтому скорость тела убывает быстрее, чем это происходило бы в отсутствие
воздуха. Вследствие этого тело, брошенное вверх с начальной скоростью , не достигает
высоты  (как это было бы
при отсутствии сопротивления) и уже на меньшей высоте начинает падать обратно.
При падении сопротивление воздуха уменьшает нарастание скорости. В результате
тело, брошенное вверх, всегда возвращается назад с меньшей скоростью, чем оно
было брошено. Таким образом, при падении на землю средняя скорость движения
меньше, чем при подъеме, и поэтому время падения на землю больше времени
подъема.

Влияние
сопротивления воздуха особенно велико при больших скоростях (так как сила
сопротивления быстро растет со скоростью). Так, например, при выстреле из винтовки
вертикально вверх пуля, вылетающая с начальной скоростью 600 м/с, должна была
бы в отсутствие воздуха достичь высоты, равной

В
действительности пуля достигает высоты только 2—3 км. При падении обратно
скорость пули возрастает лишь до 50—60 м/с. С этой предельной скоростью пуля и
достигает земли.

Суммарное сопротивление

Является суммой всех видов сил сопротивления:

X=X+Xi{\displaystyle X=X_{0}+X_{i}}

Так как сопротивление при нулевой подъёмной силе X{\displaystyle X_{0}} пропорционально квадрату скорости, а индуктивное Xi{\displaystyle X_{i}} — обратно пропорционально квадрату скорости, то они вносят разный вклад при разных скоростях. С ростом скорости X{\displaystyle X_{0}} растёт, а Xi{\displaystyle X_{i}} — падает, и график зависимости суммарного сопротивления X{\displaystyle X} от скорости («кривая потребной тяги») имеет минимум в точке пересечения кривых X{\displaystyle X_{0}} и Xi{\displaystyle X_{i}}, при которой обе силы сопротивления равны по величине. При этой скорости самолёт обладает наименьшим сопротивлением при заданной подъёмной силе (равной весу), а значит, наивысшим аэродинамическим качеством.

Мощность, требуемая для преодоления силы паразитного сопротивления, пропорциональна кубу скорости, а мощность, требуемая для преодоления индуктивного сопротивления, обратно пропорциональна скорости, поэтому суммарная мощность тоже имеет нелинейную зависимость от скорости. При некоторой скорости мощность (а значит, и расход топлива) становится минимальной — это скорость наибольшей продолжительности полёта (барражирования). Скорость, при которой достигается минимум отношения мощности (расхода топлива) к скорости полёта, является скоростью максимальной дальности полёта или крейсерской скоростью.

Интересные факты

Если не углубляться в научные знания, бытовое определение свободного перемещения подразумевает передвижение какого-либо тела в земной атмосфере, когда на него не воздействуют никакие посторонние факторы, кроме сопротивления окружающего воздуха и силы тяжести.

В различное время добровольцы соревнуются между собой, пытаясь установить личный рекорд. В 1962 г. испытатель-парашютист из СССР Евгений Андреев установил рекорд, который был занесен в Книгу рекордов Гиннеса: при прыжке с парашютом в свободном падении он преодолел расстояние в 24500 м, во время прыжка не был использован тормозной парашют.

В 1960 г. американец Д. Киттингер совершил парашютный прыжок с высоты 31 тыс. м, но с использованием парашютно-тормозной установки.

В 2005 г. была зафиксирована рекордная скорость при свободном падении — 553 км/ч, а через семь лет установлен новый рекорд — эта скорость была увеличена до 1342 км/ч. Этот рекорд принадлежит австрийскому парашютисту Феликсу Баумгартнеру, который известен во всем мире своими опасными трюками.

Сопротивление при нулевой подъёмной силе

Эта составляющая сопротивления не зависит от величины создаваемой подъёмной силы и складывается из профильного сопротивления крыла, сопротивления элементов конструкции самолёта, не вносящих вклад в подъёмную силу, и волнового сопротивления. Последнее является существенным при движении с около- и сверхзвуковой скоростью, и вызвано образованием ударной волны, уносящей значительную долю энергии движения. Волновое сопротивление возникает при достижении самолётом скорости, соответствующей критическому числу Маха, когда часть потока, обтекающего крыло самолёта, приобретает сверхзвуковую скорость. Критическое число М тем больше, чем больше угол стреловидности крыла, чем более заострена передняя кромка крыла и чем оно тоньше.

Сила сопротивления направлена против скорости движения, её величина пропорциональна характерной площади S, плотности среды ρ и квадрату скорости V:

X=CxρV22S{\displaystyle X_{0}=C_{x0}{\frac {\rho V^{2}}{2}}S}

Cx{\displaystyle C_{x0}} — безразмерный аэродинамический коэффициент сопротивления, получается из критериев подобия, например, чисел Рейнольдса и Фруда в аэродинамике.

Определение характерной площади зависит от формы тела:

• в простейшем случае (шар) — площадь поперечного сечения;
• для крыльев и оперения — площадь крыла/оперения в плане;
• для пропеллеров и несущих винтов вертолётов — либо площадь лопастей, либо ометаемая площадь винта;
• для подводных объектов обтекаемой формы — площадь смачиваемой поверхности;
• для продолговатых тел вращения, ориентированных вдоль потока (фюзеляж, оболочка дирижабля) — приведённая волюметрическая площадь, равная V2/3, где V — объём тела.

Мощность, требуемая для преодоления данной составляющей силы лобового сопротивления, пропорциональна кубу скорости (P=X⋅V=CxρV32S{\displaystyle P=X_{0}\cdot V=C_{x0}{\dfrac {\rho V^{3}}{2}}S}).