Электрическая мощность тока: как ее измерить и рассчитать

Мощность формулы. Формулы для расчета электрических величин.

Мощность и КПД в физике, формулы и примеры

Понятие мощности

Единицей измерения мощности в системе СИ является ватт.

Мощность характеризует быстроту совершения работы. Очевидно, что чем меньшее время требуется для выполнения данной работы, тем эффективнее работает машина или механизм.

В случае равномерного прямолинейного движения также справедлива формула:

где — сила, совершающая работу, — скорость движения тела.

Коэффициент полезного действия, КПД

Все механизмы или двигатели предназначены для выполнения определенной механической работы, которую называют полезной работой. Однако любой машине приходится совершать большую по величине работу, так как вследствие действия сил трения некоторая часть подводимой к машине энергии не преобразовывается в механическую работу.

Эффективность работы машины или механизма характеризуют коэффициентом полезного действия.

Коэффициент полезного действия (КПД) – это отношение полезной работы , совершенной машиной или механизмом, ко всей затраченной работе (энергии , подведенной к системе):

Также справедливы следующие формулы:

где и полезная и затраченная мощности соответственно.

Примеры решения задач

Понравился сайт? Расскажи друзьям!

Механическая мощность :: Класс!ная физика

Мощность какого подъемного механизма больше?

Мощность характеризует быстроту совершения работы.

Мощность ( N) – физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа.

Мощность показывает, какая работа совершается за единицу времени.

В Международной системе (СИ) единица мощности называется Ватт (Вт) в честь английскогоизобретателя Джеймса Ватта ( Уатта ), построившего первую паровую машину.

1 Ватт равен мощности силы, совершающей работу в 1 Дж за 1 секундуили,когда груз массой 100г поднимают на высоту 1м за 1 секунду

Сам Джеймс Уатт ( 1736 – 1819 ) пользовался другой единицей мощности – лошадиной силой ( 1 л.с. ), которую он ввел с целью возможности сравнения работоспособности паровой машины и лошади.1л.с. = 735Вт

Однако, мощность одной средней лошади – около 1/2 л.с., хотя лошади бывают разные.

“Живые двигатели” кратковременно могут повышать свою мощность в несколько раз.

Лошадь может доводить свою мощность при беге и прыжках до десятикратной и более величины.

Делая прыжок на высоту в 1м, лошадь весом 500кг развивает мощность равную 5 000 Вт = 6,8 л.с.

Считается, что в среднем мощность человека при спокойной ходьбе равна приблизительно 0,1л.с. т.е 70 – 90Вт.

При беге, прыжках человек может развивать мощность во много раз большую.

Оказывается, самым мощным источником механической энергии является огнестрельное оружие!

С помощью пушки можно бросить ядро массой 900кг со скоростью 500м/с, развивая за 0,01 секунды около 110 000 000 Дж работы. Эта работа равнозначна работе по подъему 75 т груза на вершину пирамиды Хеопса ( высота 150м ).

Мощность выстрела пушки будет составлять 11 000 000 000Вт = 15 000 000 л.с.

Сила напряжения мышц человека приблизительно равна силе тяжести, действующей на него. Когда 2 одинаковых по весу человека поднимаются по лестнице на одну высоту, но с разной скоростью, то кто из них развивает большую мощность?

эта формула справедлива для равномерного движения с постоянной скоростью и в случае переменного движения для средней скорости.

Из этих формул видно, что при постоянной мощности двигателя скорость движения обратно пропорциональна силе тяги и наоборот.На этом основан принцип действия коробки скоростей (коробки перемены передач) различных транспортных средств.

А КАК У ТЕБЯ С “СООБРАЗИЛКОЙ” ?

1. Одинаковую ли мощность развивают двигатели вагона трамвая, когда он движется с одинаковой скоростью без пассажиров и с пассажирами?

Ответ: Pri nalitshii passashiriv sila tjashesti (ves) vagona bolshe, uvelitshivaetsja sila trenia, ravnaja v dannom slutshae sile tjagi,vosrastaet motshnost, uvelitshivaetsja rashod electroenergii.

2. Почему корабль с грузом движется медленнее, чем без груза? Ведь мощность двигателя в обоих случаях одинакова.

Ответ: S uvelitsheniem nagruski korabl bolshe pogrushaetsja v wodu. eto uvelitshivaet silu soprotivlenija wodi dvisheniu korablja, tshto privodit k potere skorosti.

3. Трактор имеет три скорости:3,08; 4,18 и 5,95 км/ч . На какой скорости он будет развивать при той же мощности большую силу тяги на крюке?

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Работа определяется по формуле

1) ​ \( A=Fv \) ​ 2) \( A=N/t \) ​ 3) \( A=mv \) ​ 4) \( A=FS \) ​

2. Груз равномерно поднимают вертикально вверх за привязанную к нему верёвку. Работа силы тяжести в этом случае

1) равна нулю 2) положительная 3) отрицательная 4) больше работы силы упругости

3. Ящик тянут за привязанную к нему верёвку, составляющую угол 60° с горизонтом, прикладывая силу 30 Н. Какова работа этой силы, если модуль перемещения равен 10 м?

1) 300 Дж 2) 150 Дж 3) 3 Дж 4) 1,5 Дж

4. Искусственный спутник Земли, масса которого равна ​ \( m \) ​, равномерно движется по круговой орбите радиусом ​ \( R \) ​. Работа, совершаемая силой тяжести за время, равное периоду обращения, равна

1) ​ \( mgR \) ​ 2) ​ \( \pi mgR \) ​ 3) \( 2\pi mgR \) ​ 4) ​ \( 0 \) ​

5. Автомобиль массой 1,2 т проехал 800 м по горизонтальной дороге. Какая работа была совершена при этом силой трения, если коэффициент трения 0,1?

1) -960 кДж 2) -96 кДж 3) 960 кДж 4) 96 кДж

6. Пружину жёсткостью 200 Н/м растянули на 5 см. Какую работу совершит сила упругости при возвращении пружины в состояние равновесия?

1) 0,25 Дж 2) 5 Дж 3) 250 Дж 4) 500 Дж

7. Шарики одинаковой массы скатываются с горки по трём разным желобам, как показано на рисунке. В каком случае работа силы тяжести будет наибольшей?

1) 1 2) 2 3) 3 4) работа во всех случаях одинакова

8. Работа по замкнутой траектории равна нулю

А. Силы трения Б. Силы упругости

Верным является ответ

1) и А, и Б 2) только А 3) только Б 4) ни А, ни Б

9. Единицей мощности в СИ является

10. Чему равна полезная работа, если совершённая работа составляет 1000 Дж, а КПД двигателя 40 %?

1) 40000 Дж 2) 1000 Дж 3) 400 Дж 4) 25 Дж

11. Установите соответствие между работой силы (в левом столбце таблицы) и знаком работы (в правом столбце таблицы). В ответе запишите выбранные цифры под соответствующими буквами.

РАБОТА СИЛЫ A. Работа силы упругости при растяжении пружины Б. Работа силы трения B. Работа силы тяжести при падении тела

ЗНАК РАБОТЫ 1) положительная 2) отрицательная 3) равна нулю

12. Из приведённых ниже утверждений выберите два правильных и запишите их номера в таблицу.

1) Работа силы тяжести не зависит от формы траектории. 2) Работа совершается при любом перемещении тела. 3) Работа силы трения скольжения всегда отрицательна. 4) Работа силы упругости по замкнутому контуру не равна нулю. 5) Работа силы трения не зависит от формы траектории.

формула, мгновенный и средний расчет силы.

Термин «мощность» в физике имеет специфический смысл. Механическая работа может выполняться с различной скоростью. А механическая мощность обозначает, как быстро совершается эта работа

Способность правильно измерить мощность имеет важное значение для использования энергетических ресурсов

Физический смысл мощности

Разные виды мощности

Для формулы механической мощности применяется следующее выражение:

В числителе формулы затраченная работа, в знаменателе – временной промежуток ее совершения. Это отношение и называется мощностью.

Существует три величины, которыми можно выразить мощность: мгновенная, средняя и пиковая:

1. Мгновенная мощность – мощностной показатель, измеренный в данный момент времени. Если рассмотреть уравнение для мощности N = ΔA/Δt , то мгновенная мощность представляет собой ту, которая берется в чрезвычайно малый промежуток времени Δt. Если имеется построенная графическая зависимость мощности от времени, то мгновенная мощность – это просто считываемое с графика значение в любой взятый момент времени. Другая запись выражения для мгновенной мощности:

Средняя мощность – мощностная величина, измеренная за относительно большой временной отрезок Δt; Пиковая мощность – максимальное значение, которое мгновенная мощность может иметь в конкретной системе в течение определенного временного промежутка. Стереосистемы и двигатели автомобилей – примеры устройств, способных обеспечить максимальную мощность, намного выше их средней номинальной мощности. Однако поддерживать эту мощностную величину можно в течение короткого времени

Хотя для эксплуатационных характеристик устройств она может быть более важной, чем средняя мощность

Важно! Дифференциальная форма уравнения N = dA/dt универсальна. Если механическая работа выполняется равномерно в течение времени t, то средняя мощность будет равна мгновенной

Из общего уравнения получается запись:

где A будет общая работа за заданное время t. Тогда при равномерной работе вычисленный показатель равен мгновенной мощности, а при неравномерной –средней.

Формулы для механической мощности

В каких единицах измеряют мощность

Стандартной единицей для измерения мощности служит Ватт (Вт), названный в честь шотландского изобретателя и промышленника Джеймса Ватта. Согласно формуле, Вт = Дж/с.

Существует еще одна единица мощности, до сих пор широко используемая, – лошадиная сила (л. с.).

Интересно. Термин «лошадиная сила» берет свое начало в 17-м веке, когда лошадей использовали для поднятия груза из шахты. Одна л. с. равна мощности для поднятия 75 кг на 1 м за 1 с. Это эквивалентно 735,5 Вт.

Мощность силы

Уравнение для мощности соединяет выполненную работу и время. Поскольку известно, что работа выполняется силами, а силы могут перемещать объекты, можно получить другое выражение для мгновенной мощности:

1. Работа, проделанная силой при перемещении:

A = F x S x cos φ.

1. Если поставить А в универсальную формулу дляN, определяется мощность силы:

N = (F x S x cos φ)/t = F x V x cos φ, так как V = S/t.

1. Если сила параллельна скорости частицы, то формула принимает вид:

Мощность вращающихся объектов

Процессы, связанные с вращением объектов, могут быть описаны аналогичными уравнениями. Эквивалентом силы для вращения является крутящий момент М, эквивалент скорости V – угловая скорость ω.

Если заменить соответствующие величины, то получается формула:

M = F x r, где r – радиус вращения.

Для расчета мощности вала, вращающегося против силы, применяется формула:

где n – скорость в об/с (n = ω/2π).

Отсюда получается то же упрощенное выражение:

Таким образом, двигатель может достичь высокой мощности либо при высокой скорости, либо, обладая большим крутящим моментом. Если угловая скорость ω равна нулю, то мощность тоже равна нулю, независимо от крутящего момента.

Работа силы тяжести — разность потенциальной энергии

Рассмотрим теперь следующий пример. Яблоко массой 0,2 кг упало на садовый стол с ветки, находящейся на высоте 3 метра от поверхности земли. Столешница располагается на высоте 1 метр от поверхности (рис. 3). Найдем работу силы тяжести в этом процессе.

Посчитаем потенциальную энергию яблока до его падения и энергию яблока на столешнице.

\( E_ \left(\text \right) \) – начальная потенциальная энергия яблока;

\( E_ \left(\text \right) \) – конечная потенциальная энергия яблока;

Примечание: Работу можно рассчитать через разность потенциальной энергии тела.

Потенциальную энергию будем вычислять, используя формулу:

\[ \large E_

= m \cdot g \cdot h\]

\( m \left( \text\right) \) – масса яблока;

\( h \left( \text\right) \) – высота, на которой находится яблоко относительно поверхности земли.

Начальная высота яблока над поверхностью земли равна 3 метрам

\

Потенциальная энергия яблока на столе

\

Теперь найдем разницу потенциальной энергии яблока в конце падения и перед его началом.

\[ \large \Delta E_

= E_ — E_ \]

\[ \large \Delta E_

= 2 – 6 = — 4 \left(\text \right) \]

Важно помнить: Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!. Чтобы работа получилась положительной, в правой части формулы перед \( \Delta E_

Чтобы работа получилась положительной, в правой части формулы перед \( \Delta E_

\) дополнительно допишем знак «минус».

Значит, работа, которую потребовалось совершить силе тяжести, чтобы яблоко массой 0,2 кг упало с высоты 3 м на высоту 1 метр, равняется 4 Джоулям.

Примечания:

1. Если тело падает на землю, работа силы тяжести положительна;
2. Когда мы поднимаем тело над землей, мы совершаем работу против силы тяжести. Наша работа при этом положительна, а работа силы тяжести будет отрицательной;
3. Сила тяжести относится к консервативным силам. Для консервативных сил перед разностью потенциальной энергии мы дописываем знак «минус»;
4. Работа силы тяжести не зависит от траектории, по которой двигалось тело;
5. Работа для силы \(\displaystyle F_>\) зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени.

Рисунок 4 иллюстрирует факт, что для силы \(\displaystyle F_>\) работа зависит только от разности высот и не зависит от траектории, по которой тело двигалось.

Расчет в Excel мощности двигателя автомобиля.

Запускаем на компьютере программу MS Excel. В качестве простейшего примера рассмотрим случай равномерного длительного движения по загородной трассе небольшого легкового автомобиля, оснащенного бортовым компьютером.

Исходные данные:

Первую тройку исходных данных возьмем из показаний бортового компьютера или из замеров, выполненных любым иным способом.

1. Среднюю скорость движения автомобиля v в километрах в час запишем

в ячейку D3: 90,0

2. Пройденное расстояние S в километрах внесем

в ячейку D4: 100,0

3. Средний расход бензина V в литрах введем

4. Предположительный КПД двигателя η в процентах впишем

5. Плотность бензина ρ в килограммах на кубический метр занесем

в ячейку D7: 750

Средние значения плотностей различных марок и видов топлива:

для бензина марки АИ-80 ρ =715 кг/м 3

для бензина марки АИ-92 ρ =735 кг/м 3

для бензина марки АИ-95 ρ =750 кг/м 3

для бензина марки АИ-98 ρ =765 кг/м 3

для дизельного топлива ρ =770…840 кг/м 3

для сжиженного газа ρ =600 кг/м 3

Плотность топлива существенно зависит от температуры!

6. Удельную теплоту сгорания бензина q в мегаджоулях на килограмм запишем

Средние значения удельной теплоты сгорания различных видов топлива:

для бензина и дизельного топлива q =43 МДж/кг

для сжиженного газа ρ =45 МДж/кг

Результаты расчетов:

Выполним вывод расчетной формулы для средней мощности.

η– КПД двигателя

Q 1–полезная тепловая энергия, затраченная на перемещение автомобиля

Q 2– вся тепловая энергия, выделенная при сгорании топлива

A–работа, выполненная двигателем и затраченная на перемещение автомобиля

N–средняя мощность двигателя

S–пройденный автомобилем путь

v–средняя скорость движения автомобиля

q–удельная теплота сгорания топлива

m–масса израсходованного топлива

V–объем израсходованного топлива

p–плотность (удельная масса) топлива

Формула для расчета средней мощности двигателя автомобиля получена.

7. Вычислим среднюю мощность двигателя автомобиля N в киловаттах при заданном режиме движения

в ячейке D10: =(D6/100)*D8*1000000*D7*(D5/1000)*(D3*1000/60/60)/(D4*1000)/1000=5,241

Переведем киловатты в лошадиные силы

в ячейке D11: =D10*1000/735,49875=7,125

Теперь вы можете выполнить расчет в Excel при любых иных исходных данных и определить реально развиваемую среднюю мощность двигателя автомобиля при различных режимах движения.

Ответ на вопрос:

Для движения небольшого легкового автомобиля со скоростью 90 км/час по загородной трассе достаточно мощности двигателя всего в 7 лошадиных сил! Почти у всех автомобилей такого класса максимальная мощность двигателей превышает 80…100 лошадиных сил! Безусловно, такая мощность необходима для быстрого разгона и уверенного движения на подъемах и по дорогам с повышенным сопротивлением (грязь, снег). С мощностью двигателя в 7 лошадиных сил автомобиль до скорости 90 км/час будет разгоняться, наверное, с десяток минут…

Источник

Урок физики «Мощность»

• Познакомиться с мощностью как новой физической величиной;
• Развивать умения выводить формулы, пользуясь необходимыми знаниями прошлых уроков; развивать логическое мышление, умение анализировать, делать выводы;
• Применять знания по физике в окружающем мире.

Урок сегодня я хочу начать с вопросов к вам. (Слайд 2).

1. Как вы думаете, имеет ли какое-то отношение лошадь к физике?

2. С какой физической величиной связана лошадь?

Мощность – правильно, это и есть тема нашего урока. Запишем ее в тетрадь.

Действительно, мощность двигателей автомобилей, транспортных средств до сих пор измеряют в лошадиных силах. Сегодня на уроке мы с вами узнаем всё о мощности с точки зрения физики. Давайте подумаем вместе и определим, что мы должны знать о мощности, как о физической величине.

Существует план изучения физических величин: ( Слайд 3).

1. Определение;
2. Вектор или скаляр;
3. Буквенное обозначение;
4. Формула;
5. Прибор для измерения;
6. Единица величины.

Этот план и будут целью нашего урока.

Начнем с примера из жизни. Вам необходимо набрать бочку воды для полива растений. Вода находится в колодце. У вас есть выбор: набрать при помощи ведра или при помощи насоса. Напомню, что в обоих случаях механическая работа, совершенная при этом будет одинаковой. Конечно же, большинство из вас выберут, насос.

Вопрос: В чем разница при выполнении одной и той же работы?

Ответ: Насос выполнит эту работу быстрее, т.е. затратит меньшее время.

1) Физическая величина, характеризующая быстроту выполнения работы, называют мощностью. ( Слайд 4).

2) Скаляр, т.к. не имеет направления.

5) = [ 1 Дж/с] =

Название этой единицы мощности дано в честь английского изобретателя паровой машины (1784г) Джеймса Уатта. ( Слайд 5).

6) 1 Вт = мощности, при которой за время 1 с совершается работа в 1 Дж. ( Слайд 6).

Самолеты, автомобили, корабли и другие транспортные средства движутся часто с постоянной скоростью. Например, на трассах автомобиль достаточно долго может двигаться со скоростью 100 км/ч. ( Слайд 7).

Вопрос: от чего зависит скорость движения таких тел?

Оказывается, она напрямую зависит от мощности двигателя автомобиля.

Зная, формулу мощности мы выведем еще одну, но для этого давайте вспомним основную формулу для механической работы.

Учащийся выходит к доске для вывода формулы. ( Слайд 8).

Пусть сила совпадает по направлению со скоростью тела. Запишем формулу работы этой силы.

2.При постоянной скорости движения , тело проходит путь определяемой формулой

Подставляем в исходную формулу мощности: , получаем — мощность.

У нас получилась еще одна формула для расчета мощности, которую мы будем использовать при решении задач.

Эта формула показывает ( Слайд 9), что при постоянной мощности двигателя, изменением скорости можно менять силу тяги автомобиля и наоборот, при изменении скорости автомобиля можно менять силу тяги двигателя.

Вопрос. Когда нужна большая сила тяги?

а)При подъеме в гору. Правильно, тогда водитель снижает скорость.

б) При вспашке земли тракторист движется с малой скоростью, чтобы была большая сила тяги. Для этого водитель, тракторист, машинист, токарь, фрезеровщик часто используют коробку передач, которая позволяет менять скорость. ( Слайд 10).

Мощность всегда указывают в паспорте технического устройства. И в современных технических паспортах автомобилей есть графа:

Мощность двигателя: кВт / л.с.

Следовательно, между этими единицами мощности существует связь.

Вопрос: А откуда взялась эта единица мощности? ( Слайд 11).

Дж. Уатту принадлежит идея измерять механическую мощность в «лошадиных силах». Предложенная им единица мощности была весьма популярна, но в 1948 г. Генеральной конференцией мер и весов была введена новая единица мощности в международной системе единиц – ватт. ( Слайд 12).

1 Вт = ,00013596 л.с.

Эта единица мощности была изъята из обращения с 1 января 1980 г.

Примеры мощностей современных автомобилей. ( Слайд 13,14).

Различные двигатели имеют разные мощности.

Вопрос: А какова мощность человека?

Текс учебника, § 54. Мощность человека при нормальных условиях работы в среднем составляет 70-80 Вт. Совершая прыжки, взбегая по лестнице, человек может развивать мощность до 730 Вт, а в отдельных случаях и большую.

Вопрос: А чем «живые двигатели» отличаются от механических? ( Слайд 15).

Ответ: Тем, что «живые двигатели» могут изменять свою мощность в несколько раз.

1.Расскажите все, что вы знаете о мощности. Ответ по плану изучения физической величины.

Источник

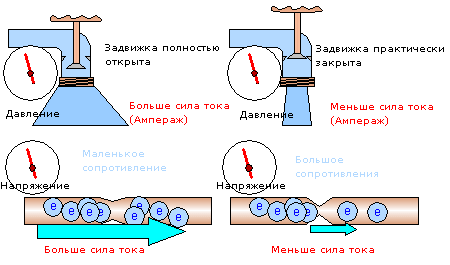
Мощность электрического тока

Для того, чтобы это показать что к чему, мы возьмем две лампы на 12 Вольт, но разной мощности. На блоке питания выставляю также 12 Вольт и собираю все это дело по схеме, которая мелькала в начале статьи

Мой блок питания может выдать в нагрузку 150 Ватт, не парясь. Беру лампочку от мопеда и цепляю ее к блоку питания

Смотрим потребление тока. 0,71 Ампер

Высчитываем сопротивление раскаленной нити лампочки из закона Ома I=U/R, отсюда R=U/I=12/0,71=16,9 Ом.

Беру галогенную лампу от фары авто и также цепляю ее к блоку питания

Смотрим потребление. 4,42 Ампера

Аналогично высчитываем сопротивление нити лампы. R=U/I=12/4,42=2,7 Ом.

А теперь давайте посчитаем, какая лампочка больше всех Ватт “отбирает”  у источника питания. Вспоминаем школьную формулу P=UI. Итак, для маленькой лампочки мощность составит P=12×0,71=8,52 Ватта. А для большой лампочки мощность  будет Р=12х4,42=53 Ватта. Ого! У нас получилось, что лампочка, которая обладала меньшим сопротивлением, на самом деле очень даже прожорливая.

Итак, если кто не помнит, что такое мощность, могу напомнить. Мощность – это отношение какой-то полезной работы к времени, в течение которого эта работа совершалась. Например, надо вскопать яму определенных размеров. Вы с лопатой, а ваш друг – на экскаваторе:

Кто быстрее справится  с задачей за  одинаковый промежуток времени? Разумеется экскаватор. В этом случае, можно сказать, что его мощность намного больше, чем мощность человека с лопатой.

А теперь представьте, что нам надо полностью под ноль сточить эту железяку:

Подумайте вот над таким вопросом… У нас есть в запасе 5 мин и нам надо сточить железяку по-максимому. В каком случае железяка сточится быстрее всего: если прижимать ее к абразивному кругу со всей дури, прижимать слегка, либо прижимать в полсилы? Не забывайте, что у нас абразивный круг подцеплен к валу, который крутит поток воды в трубе. И да, труба у нас небольшого диаметра.

Кто ответил, что если прижимать в полсилы, то оказался прав. Железяка в этом случае сточится быстрее.  Если прижимать ее со всей дури, то можно вообще остановить круг. Еще раз, что у нас такое мощность? Полезная работа, совершаемая за какой-то промежуток времени. А в нашем опыте полезная работа это и есть стачивание железяки по максималке. Также не забывайте и  тот момент, что если мы будем слегка прижимать железяку, то мы будем ее стачивать пол дня. Поэтому, золотая середина  – это давить железяку в полсилы.

Ну вот мы и снова переходим к электронике 😉

Поток воды – сила тока, давление в трубе – напряжение, давление железяки на круг – сопротивление.  И что в результате мы получили? А то, что лампочка с меньшим сопротивлением обладает большей мощностью, чем лампочка с большим сопротивлением. Не трудно догадаться, если просто посмотреть на фото, но вживую эффект лучше

Но обязательно ли то, что чем меньше сопротивление, тем больше мощности выделяется на нагрузке? Конечно же нет. Во всем нужен расчет, как  и в прошлом опыте, где мы стачивали железяку за определенное время.

И еще один фактор, конечно, тоже надо учитывать. Это давление в трубе. Прикиньте, точим-точим мы железяку, и вдруг давление в трубе стало повышаться. Может быть переполнилась башня, или кто-то открыл краник на полную катушку. Что станет с наждаком? Его обороты ускорятся,  так как сила потока воды в трубе увеличится,  а следовательно, мы еще быстрее сточим нашу железку.

Часто задаваемые вопросы

Как рассчитать мощность двигателя внутреннего сгорания?

Мощность двигателя в кВт можно рассчитать по объему двигателя и оборотах коленвала. Формула расчета мощности двигателя имеет вид: Ne = Vh * Pe * n / 120 (кВт), где: Vh — объём двигателя, см³ n — количество оборотов коленчатого вала за минуту Pe — среднее эффективное давление, Мпа

Какой коэффициент учитывать при расчете мощности двигателя?

Коэффициент мощности (cosϕ) для расчета мощности электродвигателя принимают равным 0,8 для маломощных двигателей (менее 5,5 кВт) или 0,9 для двигателей мощностью свыше 15 кВт.

Как рассчитать мощность двигателя по крутящему моменту?

Для определения мощности двигателя в киловаттах, когда известен крутящий момент, можно по формуле такого вида: P = Mкр * n/9549, где: Mкр – крутящий момент (Нм), n – обороты коленвала (об./мин.), 9549 – коэффициент для перевода оборотов в об/мин.

Как рассчитать мощность двигателя по расходу воздуха?

Рассчитать мощность двигателя в кВт зная его потребления воздуха (при наличии бортового компьютера) можно используя простую схему. Необходимо раскрутить двигатель на третьей передаче до 5500 об/мин (пик крутящего момента) и по показаниям, на тот момент, зафиксировать расход воздуха, а затем разделить то значение на три. В результате такого математического вычисления можно узнать приблизительную мощность двигателя с небольшой погрешностью.

Источник

Урок физики «Мощность»

• Познакомиться с мощностью как новой физической величиной;
• Развивать умения выводить формулы, пользуясь необходимыми знаниями прошлых уроков; развивать логическое мышление, умение анализировать, делать выводы;
• Применять знания по физике в окружающем мире.

Урок сегодня я хочу начать с вопросов к вам. (Слайд 2).

1. Как вы думаете, имеет ли какое-то отношение лошадь к физике?

2. С какой физической величиной связана лошадь?

Мощность – правильно, это и есть тема нашего урока. Запишем ее в тетрадь.

Действительно, мощность двигателей автомобилей, транспортных средств до сих пор измеряют в лошадиных силах. Сегодня на уроке мы с вами узнаем всё о мощности с точки зрения физики. Давайте подумаем вместе и определим, что мы должны знать о мощности, как о физической величине.

Существует план изучения физических величин: ( Слайд 3).

1. Определение;
2. Вектор или скаляр;
3. Буквенное обозначение;
4. Формула;
5. Прибор для измерения;
6. Единица величины.

Этот план и будут целью нашего урока.

Начнем с примера из жизни. Вам необходимо набрать бочку воды для полива растений. Вода находится в колодце. У вас есть выбор: набрать при помощи ведра или при помощи насоса. Напомню, что в обоих случаях механическая работа, совершенная при этом будет одинаковой. Конечно же, большинство из вас выберут, насос.

Вопрос: В чем разница при выполнении одной и той же работы?

Ответ: Насос выполнит эту работу быстрее, т.е. затратит меньшее время.

1) Физическая величина, характеризующая быстроту выполнения работы, называют мощностью. ( Слайд 4).

2) Скаляр, т.к. не имеет направления.

5) = [ 1 Дж/с] =

Название этой единицы мощности дано в честь английского изобретателя паровой машины (1784г) Джеймса Уатта. ( Слайд 5).

6) 1 Вт = мощности, при которой за время 1 с совершается работа в 1 Дж. ( Слайд 6).

Самолеты, автомобили, корабли и другие транспортные средства движутся часто с постоянной скоростью. Например, на трассах автомобиль достаточно долго может двигаться со скоростью 100 км/ч. ( Слайд 7).

Вопрос: от чего зависит скорость движения таких тел?

Оказывается, она напрямую зависит от мощности двигателя автомобиля.

Зная, формулу мощности мы выведем еще одну, но для этого давайте вспомним основную формулу для механической работы.

Учащийся выходит к доске для вывода формулы. ( Слайд 8).

Пусть сила совпадает по направлению со скоростью тела. Запишем формулу работы этой силы.

2.При постоянной скорости движения , тело проходит путь определяемой формулой

Подставляем в исходную формулу мощности: , получаем — мощность.

У нас получилась еще одна формула для расчета мощности, которую мы будем использовать при решении задач.

Эта формула показывает ( Слайд 9), что при постоянной мощности двигателя, изменением скорости можно менять силу тяги автомобиля и наоборот, при изменении скорости автомобиля можно менять силу тяги двигателя.

Вопрос. Когда нужна большая сила тяги?

а)При подъеме в гору. Правильно, тогда водитель снижает скорость.

б) При вспашке земли тракторист движется с малой скоростью, чтобы была большая сила тяги. Для этого водитель, тракторист, машинист, токарь, фрезеровщик часто используют коробку передач, которая позволяет менять скорость. ( Слайд 10).

Мощность всегда указывают в паспорте технического устройства. И в современных технических паспортах автомобилей есть графа:

Мощность двигателя: кВт / л.с.

Следовательно, между этими единицами мощности существует связь.

Вопрос: А откуда взялась эта единица мощности? ( Слайд 11).

Дж. Уатту принадлежит идея измерять механическую мощность в «лошадиных силах». Предложенная им единица мощности была весьма популярна, но в 1948 г. Генеральной конференцией мер и весов была введена новая единица мощности в международной системе единиц – ватт. ( Слайд 12).

1 Вт = ,00013596 л.с.

Эта единица мощности была изъята из обращения с 1 января 1980 г.

Примеры мощностей современных автомобилей. ( Слайд 13,14).

Различные двигатели имеют разные мощности.

Вопрос: А какова мощность человека?

Текс учебника, § 54. Мощность человека при нормальных условиях работы в среднем составляет 70-80 Вт. Совершая прыжки, взбегая по лестнице, человек может развивать мощность до 730 Вт, а в отдельных случаях и большую.

Вопрос: А чем «живые двигатели» отличаются от механических? ( Слайд 15).

Ответ: Тем, что «живые двигатели» могут изменять свою мощность в несколько раз.

1.Расскажите все, что вы знаете о мощности. Ответ по плану изучения физической величины.

Источник

Работа — разность кинетической энергии

Работу можно рассчитать еще одним способом — измеряя кинетическую энергию тела в начале и в конце процесса движения. Рассмотрим такой пример. Пусть автомобиль, движется по горизонтальной прямой и, при этом увеличивает свою скорость (рис. 2). Масса автомобиля 1000 кг. В начале его скорость равнялась 1 м/с. После разгона скорость автомобиля равна 10 метрам в секунду. Найдем работу, которую пришлось проделать, чтобы ускорить этот автомобиль.

Для этого посчитаем энергию движения автомобиля в начале и в конце разгона.

\( E_ \left(\text \right) \) – начальная кинетическая энергия машины;

\( E_ \left(\text \right) \) – конечная кинетическая энергия машины;

\( m \left( \text\right) \) – масса автомобиля;

\( \displaystyle v \left( \frac>\right) \) – скорость, с которой машина движется.

Кинетическую энергию будем вычислять, используя формулу:

\

\

Теперь найдем разницу кинетической энергии в конце и вначале разгона.

\

\

Значит, работа, которую потребовалось совершить, чтобы разогнать машину массой 1000 кг от скорости 1 м/с до скорости 10 м/с, равняется 49500 Джоулям.

Примечание: Работа – это разность энергии в конце процесса и в его начале. Можно находить разность кинетической энергии, а можно — разность энергии потенциальной.